For Problem 3, calculate the tension force T in the cable [N]. For Problem 3, calculate the support reaction Ax [N]. For Problem 3, calculate the support reaction Ay [N].
Understand the Problem
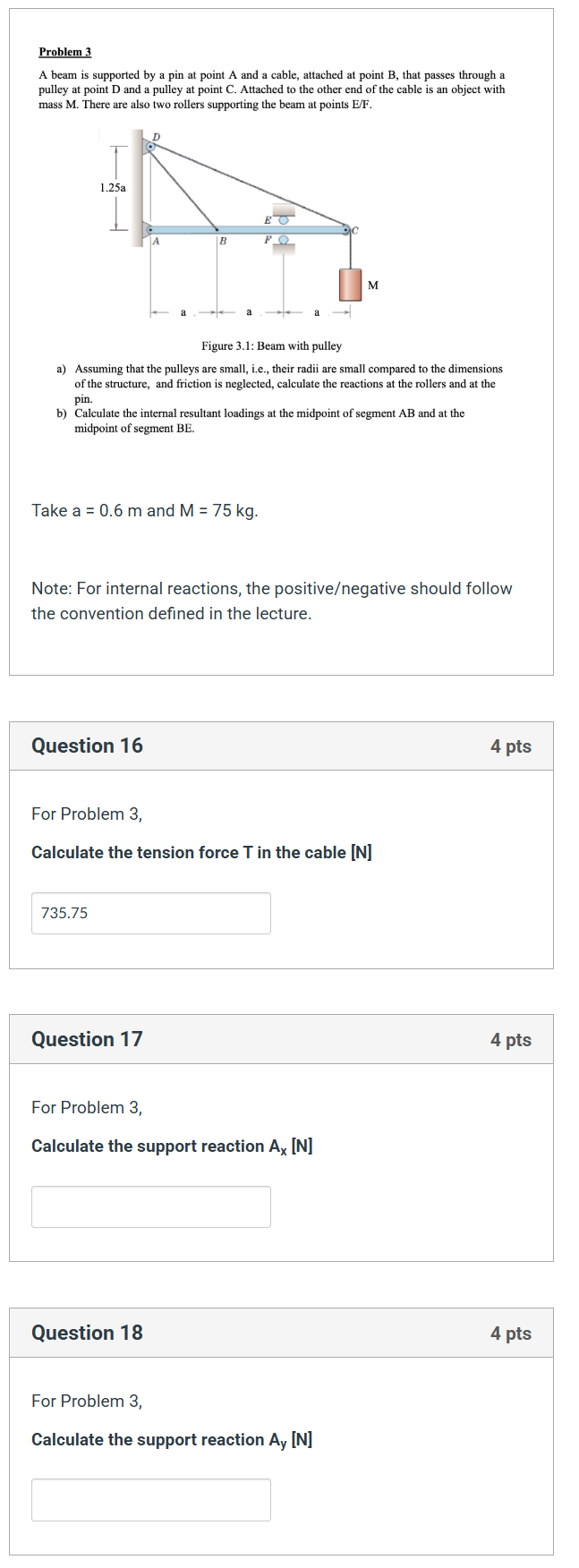
The question is asking to calculate specific forces and reactions in a mechanical structure involving a beam, pulleys, and a mass. It requires applying principles of static equilibrium to determine these values.
Answer
- Tension \( T = 735.75 \, \text{N} \) - Support reactions \( A_x \) and \( A_y\) depend on tension and weight.
Answer for screen readers
- Tension force ( T = 735.75 , \text{N} )
- Support reaction ( A_x = T \cdot \cos(\theta) )
- Support reaction ( A_y = W - T \cdot \sin(\theta) )
Steps to Solve
-
Calculate the Weight of the Mass First, calculate the force due to the mass ( M ): $$ W = M \cdot g $$ where ( g ) is the acceleration due to gravity (approximately ( 9.81 , \text{m/s}^2 )). Substituting the values: $$ W = 75 , \text{kg} \cdot 9.81 , \text{m/s}^2 = 735.75 , \text{N} $$
-
Resolving Forces at the Pin Support Use static equilibrium conditions. The sum of vertical forces must equal zero: $$ \sum F_y = 0 \implies A_y + T \cdot \sin(\theta) - W = 0 $$ Where ( T ) is the tension in the cable and ( \theta ) can be determined from the geometry. The horizontal sum gives: $$ \sum F_x = 0 \implies A_x - T \cdot \cos(\theta) = 0 $$
-
Calculating the Angle ( \theta ) Determine the angle ( \theta ) using the geometry:
- The horizontal distance ( a = 0.6 , \text{m} ) and vertical distance ( 1.25a = 0.75 , \text{m} ). The tangent gives: $$ \tan(\theta) = \frac{1.25a}{a} = \frac{1.25}{1} $$ $$ \theta = \tan^{-1}(1.25) $$
- Substituting ( T ) into Equations Now, substitute ( T ) from the tension equation back into the vertical and horizontal equilibrium equations:
- From the vertical equation, calculate ( A_y ): $$ A_y = W - T \cdot \sin(\theta) $$
- From the horizontal equation, calculate ( A_x ): $$ A_x = T \cdot \cos(\theta) $$
- Calculating Tension and Reactions Solve for ( T ) using the previously calculated weight: Substituting values and solving for both reactions ( A_x ) and ( A_y ):
- Calculate ( A_y ) using the previously computed ( T ) and ( W ).
- Then calculate ( A_x ) using the ( T ) value determined.
- Tension force ( T = 735.75 , \text{N} )
- Support reaction ( A_x = T \cdot \cos(\theta) )
- Support reaction ( A_y = W - T \cdot \sin(\theta) )
More Information
The calculations use principles of static equilibrium, where forces acting on the beam result in a net force of zero. This ensures the beam maintains its position without moving.
Tips
- Forgetting to consider the direction of tension or weight in calculations.
- Not correctly computing ( \theta ) from the geometry.
- Mixing up which force is acting in the horizontal or vertical direction.
AI-generated content may contain errors. Please verify critical information