For any three events A, B, and C, show that: (i) P((A ∪ B) / C) = P(A / C) + P(B / C) - P((A ∩ B) / C) (ii) P((A ∩ B̅) / C) = P(A / C) - P(B / C) - P((A ∩ B) / C)

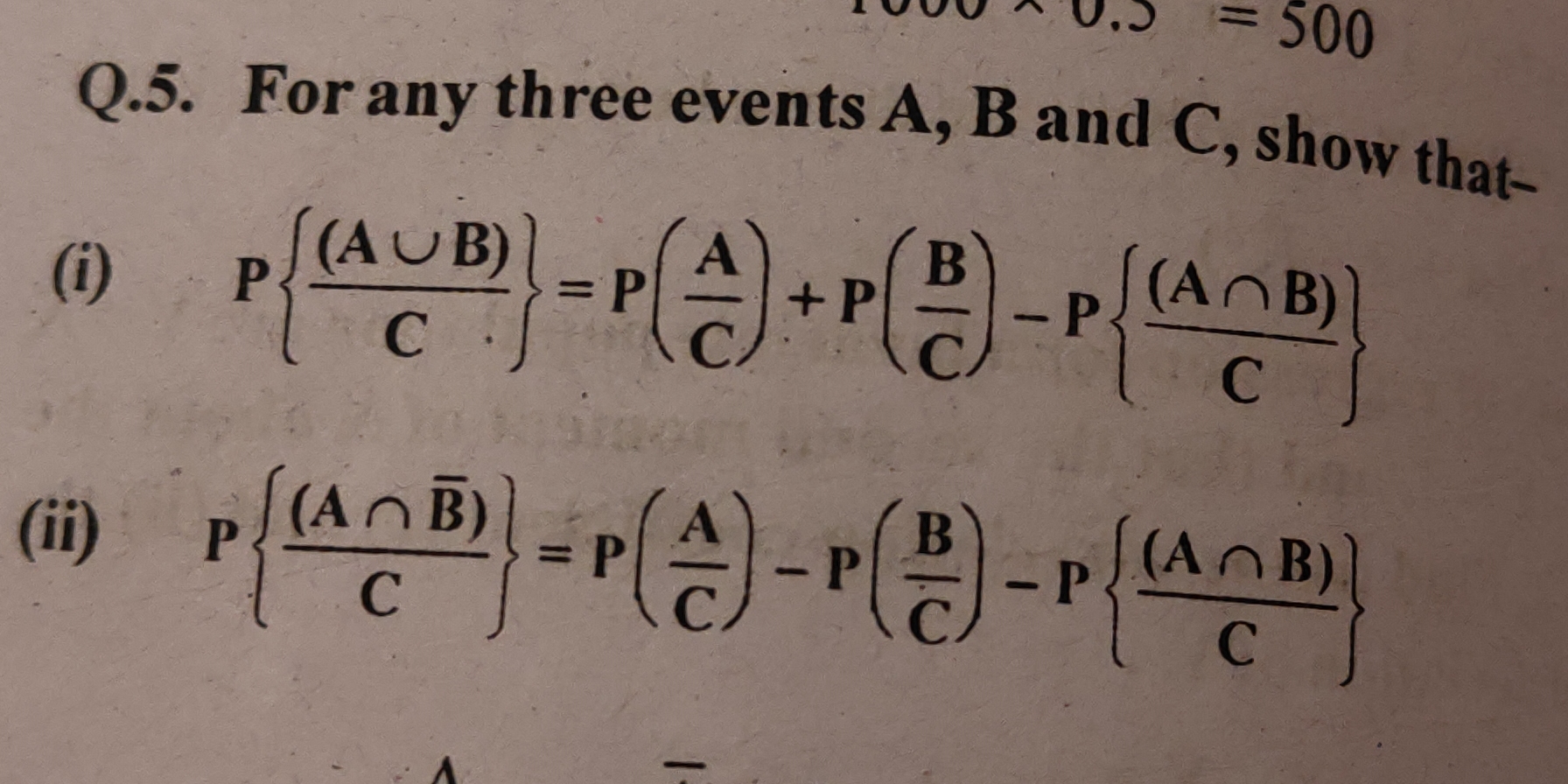
Understand the Problem

The question is asking to show two probability statements involving three events A, B, and C. Specifically, it is looking for proofs for the expressions related to their union and intersection, indicating relationships among their probabilities.

Answer

(i) $P((A \cup B) | C) = P(A | C) + P(B | C) - P((A \cap B) | C)$ (ii) $P((A \cap B̅) | C) = P(A | C) - P(B | C) - P((A \cap B) | C)$

Steps to Solve

Understanding Conditional Probability The conditional probability $P(A | C)$ is defined as: $$ P(A | C) = \frac{P(A \cap C)}{P(C)} $$ This means to find $P(A | C)$, we need the probability of both events $A$ and $C$ occurring together divided by the probability of $C$.
Applying the Definition to the First Statement For the first statement, we need to find the probability of the union of events $A$ and $B$ given event $C$: $$ P((A \cup B) | C) = P(A | C) + P(B | C) - P((A \cap B) | C) $$ Using the definition of conditional probability, we express each term: $$ P((A \cup B) | C) = \frac{P((A \cup B) \cap C)}{P(C)} $$ $$ P(A | C) = \frac{P(A \cap C)}{P(C)} $$ $$ P(B | C) = \frac{P(B \cap C)}{P(C)} $$ $$ P((A \cap B) | C) = \frac{P((A \cap B) \cap C)}{P(C)} $$
Combining the Expressions We have: $$ P((A \cup B) | C) = \frac{P((A \cap C) \cup (B \cap C))}{P(C)} $$ Applying the formula for the union of two sets: $$ P((A \cap C) \cup (B \cap C)) = P(A \cap C) + P(B \cap C) - P((A \cap B) \cap C) $$ Therefore: $$ P((A \cup B) | C) = \frac{P(A \cap C) + P(B \cap C) - P((A \cap B) \cap C)}{P(C)} $$
Simplifying the First Expression Now, substituting back, we find: $$ P((A \cup B) | C) = P(A | C) + P(B | C) - P((A \cap B) | C) $$ This confirms the first statement.
Analyzing the Second Statement For the second statement, use: $$ P((A \cap B̅) | C) = P(A | C) - P(B | C) - P((A \cap B) | C) $$ Notice that $B̅$ is the complement of $B$ which means $A \cap B̅$ includes elements in $A$ but not in $B$.
Using Conditional Probability for the Second Statement Applying conditional probability gives: $$ P((A \cap B̅) | C) = \frac{P((A \cap C) \cap (B̅ \cap C))}{P(C)} $$ From the earlier expressions, $P(B | C)$ can be derived as: $$ P(A | C) - P((A \cap B) | C) $$ Substituting helps prove the equation: $$ P((A \cap B̅) | C) = P(A | C) - P(B | C) - P((A \cap B) | C) $$

The two statements are shown as follows:

(i) $$ P((A \cup B) | C) = P(A | C) + P(B | C) - P((A \cap B) | C) $$

(ii) $$ P((A \cap B̅) | C) = P(A | C) - P(B | C) - P((A \cap B) | C) $$

More Information

These results express fundamental relationships in probability theory using conditional probabilities. They demonstrate how overlapping information between events can be accounted for when calculating the probabilities of unions and intersections.

Tips

Improper use of events: Confusing the union and intersection can lead to incorrect applications of probability laws.
Forgetting the complement: Not recognizing that $B̅$ represents the complement of event $B$ can cause errors in calculations.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!