For a free particle, the total energy is E = p²/2m. This becomes in the de Broglie formulation: ωħ = ħ²k²/2m. Explain or derive the implications of these equations.
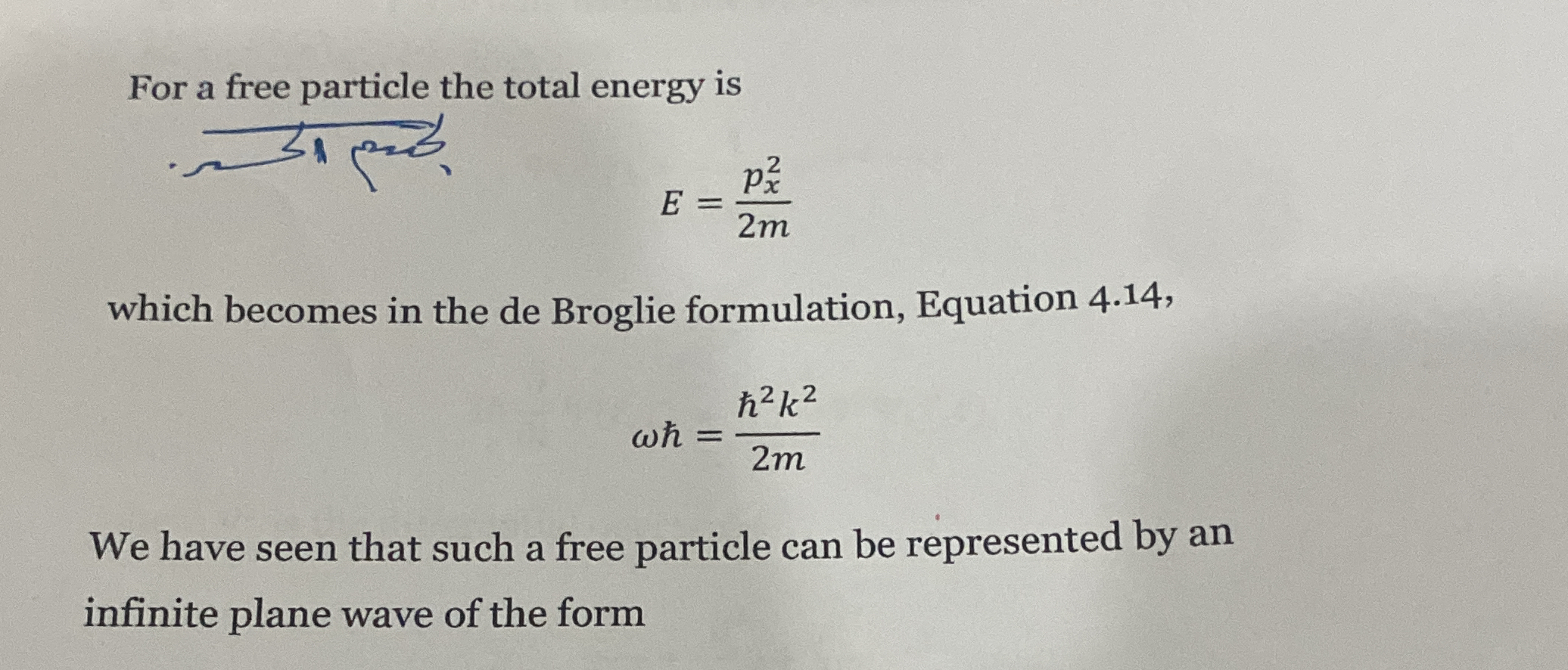
Understand the Problem
The question seems to discuss the total energy of a free particle in the context of quantum mechanics, specifically referencing the de Broglie wavelength and the equation relating energy and momentum.
Answer
E = p²/2m transforms to ħω = ħ²k²/2m using de Broglie relations.
The conversion of E = p²/2m to ħω = ħ²k²/2m using de Broglie relations shows the wave-particle duality, linking particle momentum with wave characteristics.
Answer for screen readers
The conversion of E = p²/2m to ħω = ħ²k²/2m using de Broglie relations shows the wave-particle duality, linking particle momentum with wave characteristics.
More Information
This derivation demonstrates the core concept of wave-particle duality and is foundational for understanding quantum mechanics concepts, such as particle waves.
Tips
Be careful with units and constants. Ensure that ħ is correctly applied when moving between classical and quantum expressions.
Sources
- 13.3: Free Particles and the de Broglie Wavelength - phys.libretexts.org
AI-generated content may contain errors. Please verify critical information