f(n) = n / (n - 5)

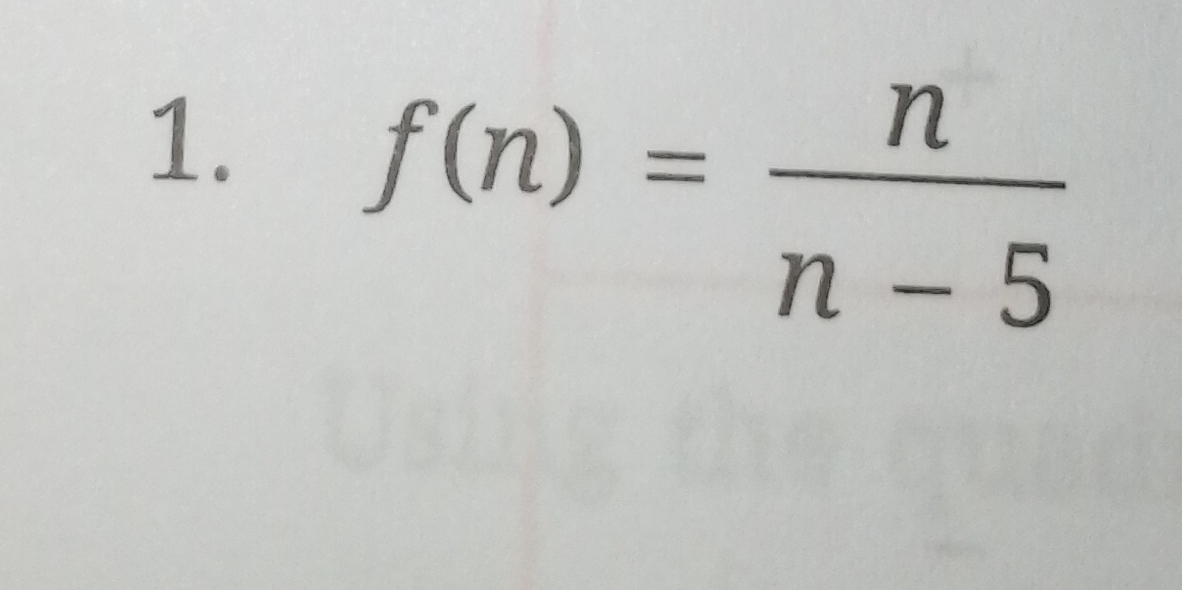
Understand the Problem

The question presents a function f(n) defined as the ratio of n to (n - 5). It is likely seeking an analysis or further calculation related to this function.

Answer

The function has a vertical asymptote at $ n = 5 $ and a horizontal asymptote at $ y = 1 $.

Steps to Solve

Identify the function The function is given as ( f(n) = \frac{n}{n - 5} ).
Determine the domain To find where the function is not defined, set the denominator to zero: $$ n - 5 = 0 $$ This implies ( n = 5 ). Therefore, the function is undefined at ( n = 5 ).
Evaluate limits at critical points To analyze the behavior near the excluded value:

As ( n \to 5^+ ), ( f(n) \to +\infty )
As ( n \to 5^- ), ( f(n) \to -\infty )

Find intercepts

Y-intercept: Set ( n = 0 ) $$ f(0) = \frac{0}{0 - 5} = 0 $$ So the y-intercept is at ( (0, 0) ).
X-intercept: Set ( f(n) = 0 ) $$ \frac{n}{n - 5} = 0 $$ This occurs when ( n = 0 ). Therefore, the x-intercept is at ( (0, 0) ).

Analyze end behavior

As ( n \to \infty ): $$ f(n) \to 1 $$
As ( n \to -\infty ): $$ f(n) \to 1 $$

Summarize findings The function has a vertical asymptote at ( n = 5 ) and horizontal asymptote at ( y = 1 ).

The function ( f(n) = \frac{n}{n - 5} ) has a vertical asymptote at ( n = 5 ), a horizontal asymptote at ( y = 1 ), and an intercept at ( (0, 0) ).

More Information

This function is a hyperbola. Hyperbolas often have vertical and horizontal asymptotes. The value ( n = 5 ) is critical because the function is undefined there.

Tips

Confusing the behavior of the function near the vertical asymptote. It is important to differentiate between approaching from the positive and negative sides.
Not finding the intercepts correctly. Remember to evaluate where the function is zero and where the input itself is zero.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!