Find x if [x 1] * [[1, 0], [-2, -3]] * [x, 3] = 0
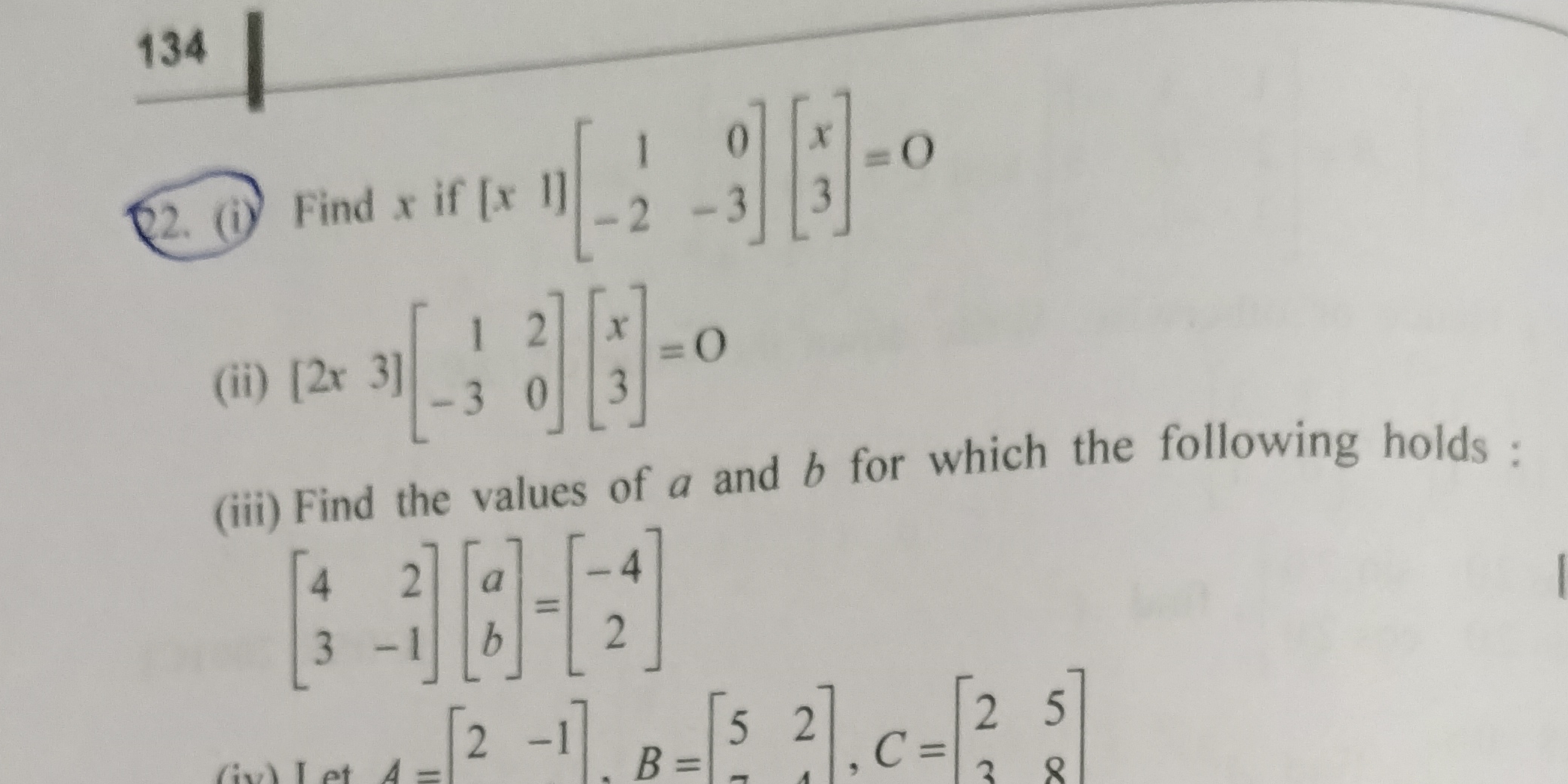
Understand the Problem
The question asks to solve for x in the matrix equation [x 1] * [[1, 0], [-2, -3]] * [x, 3] = 0. This involves matrix multiplication and solving the resulting equation.
Answer
$x = 1 \pm \sqrt{10}$
Answer for screen readers
$x = 1 + \sqrt{10}$ or $x = 1 - \sqrt{10}$
Steps to Solve
- Perform the first matrix multiplication Multiply the matrix $\begin{bmatrix} x & 1 \end{bmatrix}$ by the matrix $\begin{bmatrix} 1 & 0 \ -2 & -3 \end{bmatrix}$:
$$ \begin{bmatrix} x & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 \ -2 & -3 \end{bmatrix} = \begin{bmatrix} x(1) + 1(-2) & x(0) + 1(-3) \end{bmatrix} = \begin{bmatrix} x-2 & -3 \end{bmatrix} $$
- Perform the second matrix multiplication Multiply the resulting matrix $\begin{bmatrix} x-2 & -3 \end{bmatrix}$ by the matrix $\begin{bmatrix} x \ 3 \end{bmatrix}$:
$$ \begin{bmatrix} x-2 & -3 \end{bmatrix} \begin{bmatrix} x \ 3 \end{bmatrix} = (x-2)(x) + (-3)(3) = x^2 - 2x - 9 $$
- Solve the quadratic equation Set the result equal to 0 and solve for $x$: $$ x^2 - 2x - 9 = 0 $$ Use the quadratic formula to solve for $x$: $$ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} $$ where $a = 1$, $b = -2$, and $c = -9$.
$$ x = \frac{-(-2) \pm \sqrt{(-2)^2 - 4(1)(-9)}}{2(1)} = \frac{2 \pm \sqrt{4 + 36}}{2} = \frac{2 \pm \sqrt{40}}{2} = \frac{2 \pm 2\sqrt{10}}{2} = 1 \pm \sqrt{10} $$
$x = 1 + \sqrt{10}$ or $x = 1 - \sqrt{10}$
More Information
The problem involves matrix multiplication and solving a quadratic equation. The quadratic formula is a standard method for finding the roots of any quadratic equation.
Tips
A common mistake is an error while performing the matrix multiplication or misapplying the quadratic formula. Checking the arithmetic is essential.
AI-generated content may contain errors. Please verify critical information