Find the volume of the solid whose base is the semicircle y = √(25 - x²) where -5 ≤ x ≤ 5 and the cross sections perpendicular to the x-axis are squares.
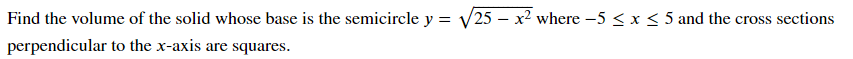
Understand the Problem
The question is asking to calculate the volume of a solid whose base is defined by the semicircle equation and has square cross-sections perpendicular to the x-axis within the specified x range.
Answer
The volume of the solid is $V = \frac{2000}{3}$ cubic units.
Answer for screen readers
The volume of the solid is given by: $$ V = \frac{2000}{3} \text{ cubic units} $$
Steps to Solve
- Define the Geometry of the Problem
The area of the cross-section is defined by the square with its base on the semicircle. The side length $s$ of the square corresponds to the diameter of the semicircle at any point $x$, which is $2y$.
- Express the Side Length in Terms of x
Since the semicircle's equation is given by $y = \sqrt{25 - x^2}$, the side length of the square cross-section can be calculated as: $$ s = 2y = 2\sqrt{25 - x^2} $$
- Calculate the Area of the Cross-section
The area $A$ of the square cross-section is given by: $$ A = s^2 = (2\sqrt{25 - x^2})^2 $$ Expanding this gives: $$ A = 4(25 - x^2) = 100 - 4x^2 $$
- Set Up the Integral for Volume
To find the volume $V$ of the solid, we need to integrate the area of the cross-section from $x = -5$ to $x = 5$: $$ V = \int_{-5}^{5} A , dx = \int_{-5}^{5} (100 - 4x^2) , dx $$
- Evaluate the Integral
Calculate the integral: $$ V = \int_{-5}^{5} (100 - 4x^2) , dx = \left[100x - \frac{4x^3}{3}\right]_{-5}^{5} $$
Evaluating from $-5$ to $5$:
- At $x = 5$: $$ 100(5) - \frac{4(5)^3}{3} = 500 - \frac{500}{3} = \frac{1500 - 500}{3} = \frac{1000}{3} $$
- At $x = -5$ (the same calculation gives the same result): $$ 100(-5) - \frac{4(-5)^3}{3} = -500 + \frac{500}{3} = -\frac{1500 - 500}{3} = -\frac{1000}{3} $$ Thus, the total volume is: $$ V = \left[\frac{1000}{3} - (-\frac{1000}{3})\right] = \frac{2000}{3} $$
The volume of the solid is given by: $$ V = \frac{2000}{3} \text{ cubic units} $$
More Information
This solid has a volume of $\frac{2000}{3}$ cubic units, illustrating how the integration of area can yield the total volume by considering the varying cross-sectional area along a defined axis.
Tips
- Ignoring the absolute value: When calculating square lengths, ensure not to ignore positive dimensions.
- Incorrect integration limits: Always double-check that the limits of integration correspond to the correct area on the x-axis.
AI-generated content may contain errors. Please verify critical information