Find the volume of the solid generated by rotating the region bounded by x=0, y=10, and y=x+2 about the line y=-1 using: a) the cylindrical shell method. b) the washer method.

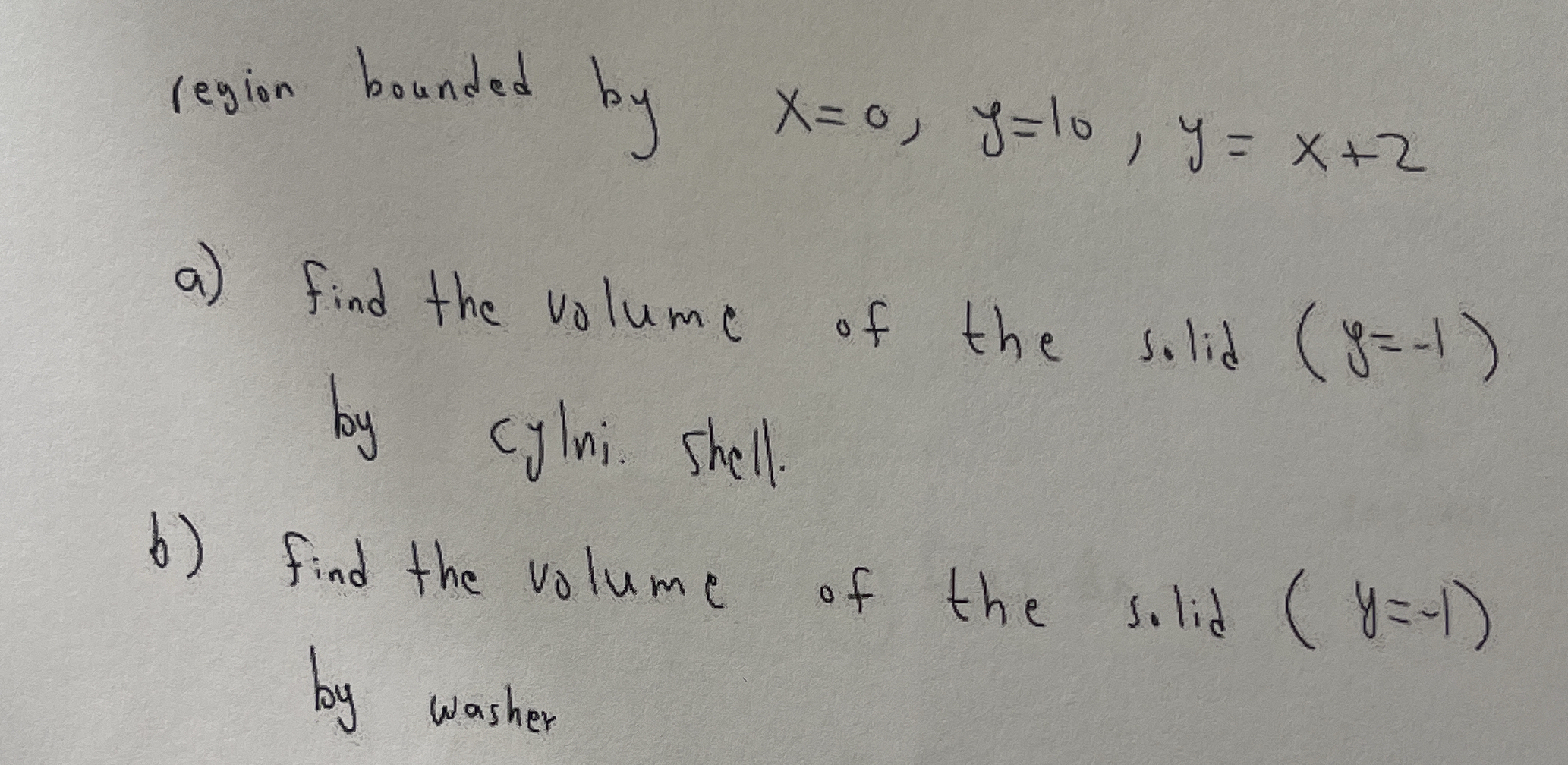
Understand the Problem

The question asks to find the volume of a solid generated by rotating a region bounded by the lines x=0, y=10, and y=x+2 around the line y=-1. Part (a) requires using the cylindrical shell method, while part (b) requires using the washer method.

Answer

a) $V = \frac{1600\pi}{3}$ b) $V = \frac{1600\pi}{3}$

Steps to Solve

Find the intersection points of the bounding curves

First, we need to find where the lines $y=10$ and $y=x+2$ intersect. Set them equal to each other: $10 = x + 2$, so $x = 8$. Thus, the intersection point is $(8, 10)$. We also have the line $x = 0$. The line $y = x+2$ intersects $x=0$ at the point $(0, 2)$. The line $y=10$ intersects $x=0$ at the point $(0, 10)$.

Part (a): Cylindrical Shell Method

Since we're rotating around $y = -1$, we'll integrate with respect to $y$. The radius of a cylindrical shell is $y - (-1) = y + 1$. The height of the cylindrical shell is the $x$ distance, which is $x = y - 2$ on the right and $x = 0$ on the left, so the height is $(y - 2) - 0 = y - 2$. The limits of integration are from $y = 2$ to $y = 10$.

Set up the integral: $$ V = 2\pi \int_{2}^{10} (y + 1)(y - 2) , dy $$

Evaluate the integral for the cylindrical shell method

Expand the integrand: $(y + 1)(y - 2) = y^2 - 2y + y - 2 = y^2 - y - 2$.

Now, integrate: $$ V = 2\pi \int_{2}^{10} (y^2 - y - 2) , dy = 2\pi \left[ \frac{1}{3}y^3 - \frac{1}{2}y^2 - 2y \right]_{2}^{10} $$

Evaluate at the limits: $$ V = 2\pi \left[ \left( \frac{1000}{3} - \frac{100}{2} - 20 \right) - \left( \frac{8}{3} - \frac{4}{2} - 4 \right) \right] $$ $$ V = 2\pi \left[ \frac{1000}{3} - 50 - 20 - \frac{8}{3} + 2 + 4 \right] $$ $$ V = 2\pi \left[ \frac{992}{3} - 64 \right] = 2\pi \left[ \frac{992 - 192}{3} \right] = 2\pi \left[ \frac{800}{3} \right] = \frac{1600\pi}{3} $$

Part (b): Washer Method

Since we're rotating around $y = -1$, we'll integrate with respect to $x$. The outer radius is $10 - (-1) = 11$, and the inner radius is $(x + 2) - (-1) = x + 3$. The limits of integration are from $x = 0$ to $x = 8$.

Set up the integral: $$ V = \pi \int_{0}^{8} (11^2 - (x + 3)^2) , dx $$

Evaluate the integral for the washer method

Expand the integrand: $11^2 - (x + 3)^2 = 121 - (x^2 + 6x + 9) = 121 - x^2 - 6x - 9 = 112 - x^2 - 6x$. Now, integrate: $$ V = \pi \int_{0}^{8} (112 - x^2 - 6x) , dx = \pi \left[ 112x - \frac{1}{3}x^3 - 3x^2 \right]_{0}^{8} $$

Evaluate at limits: $$ V = \pi \left[ 112(8) - \frac{1}{3}(8^3) - 3(8^2) \right] -0 $$ $$ V = \pi \left[ 896 - \frac{512}{3} - 192 \right] = \pi \left[ 704 - \frac{512}{3} \right] = \pi \left[ \frac{2112 - 512}{3} \right] = \pi \left[ \frac{1600}{3} \right] = \frac{1600\pi}{3} $$

a) $V = \frac{1600\pi}{3}$ b) $V = \frac{1600\pi}{3}$

More Information

Both methods yield the same volume, as expected. This confirms the correctness of the calculations.

Tips

Forgetting to add 1 to the radius when rotating around $y = -1$.
Incorrectly setting up the limits of integration.
Making algebraic errors when expanding and simplifying the integrand.
Incorrectly applying the formulas for the cylindrical shell and washer methods.