Find the volume of the prism whose base is the triangle in the xy-plane bounded by the x-axis and the lines y = x and x = 1 and whose top lies in the plane z = f(x, y) = 3 - x - y.
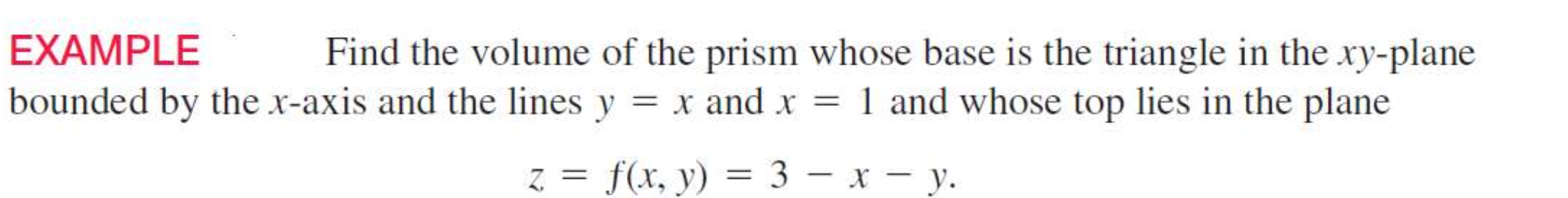
Understand the Problem
The question is asking to find the volume of a prism. The base of the prism is defined by a triangle in the xy-plane, which is bounded by the x-axis and specific lines, while the top surface is defined by a function of x and y. To solve this, we will set up the integral that represents the volume based on the given boundaries and the function.
Answer
The volume of the prism is $1$.
Answer for screen readers
The volume of the prism is $1$.
Steps to Solve
-
Identify the region of integration
The base of the prism is defined by the triangle bounded by the x-axis, the line $y = x$, and the line $x = 1$. The vertices of the triangle are (0,0), (1,0), and (1,1). -
Set up the double integral for volume
The volume $V$ of the prism can be found using the double integral over the region $R$ and the function $z = f(x,y) = 3 - x - y$.The integral is given by: $$ V = \iint_R (3 - x - y) , dA $$
-
Define the limits of integration
The limits of integration for $y$ will be from the x-axis ($y = 0$) to the line $y = x$. The limits for $x$ will be from 0 to 1. Thus, the integral becomes: $$ V = \int_0^1 \int_0^x (3 - x - y) , dy , dx $$ -
Evaluate the inner integral
Evaluate the inner integral with respect to $y$: $$ \int_0^x (3 - x - y) , dy $$ The result of this integral is: $$ (3 - x)y - \frac{y^2}{2} \bigg|_0^x = (3 - x)x - \frac{x^2}{2} $$ -
Simplify the expression
This results in: $$ V = \int_0^1 \left((3 - x)x - \frac{x^2}{2}\right) , dx $$ -
Evaluate the outer integral
Now evaluate the outer integral: $$ V = \int_0^1 \left(3x - x^2 - \frac{x^2}{2}\right) , dx $$
Simplifying this yields: $$ V = \int_0^1 (3x - \frac{3x^2}{2}) , dx $$ -
Calculate the integral
Calculate: $$ \int_0^1 \left(3x - \frac{3x^2}{2}\right) , dx = \frac{3x^2}{2} - \frac{3x^3}{6} \bigg|_0^1 = \frac{3}{2} - \frac{1}{2} = 1 $$
The volume of the prism is $1$.
More Information
The volume of a prism can be calculated by finding the area of the base and then multiplying it by the height. In this case, the height is determined by the function $z = 3 - x - y$.
Tips
- Incorrect limits of integration: It's essential to carefully analyze the bounded region to set up the correct limits. Always visualize the triangle to confirm.
- Miscalculating the inner integral: Ensure you keep track of all terms while integrating.
AI-generated content may contain errors. Please verify critical information