Find the volume of the largest right circular cone that can be inscribed in a sphere of radius 3.

Steps to Solve

1. Identify the dimensions of the cone

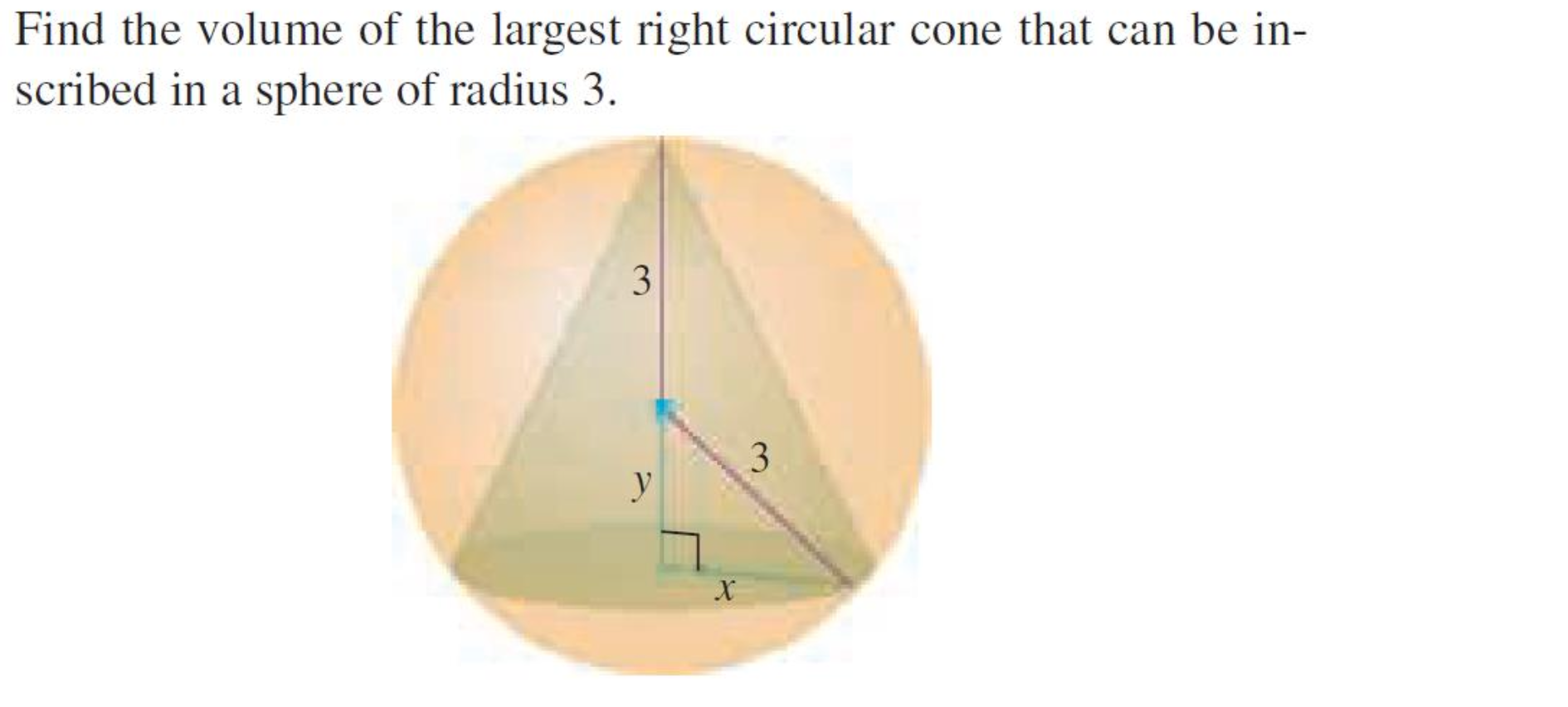
   Let the height of the cone be $h$ and the radius of the circular base be $r$. According to the problem, the sphere has a radius of 3. We can relate the height $h$ and the base radius $r$ using the Pythagorean theorem.

2. Relate the cone's dimensions to the sphere's radius

   In the diagram, we have a vertical height $y$ (from the apex of the cone to the center of the sphere) and a distance $x$ (from the center of the sphere to the bottom of the cone). The total height relates as follows: [ h = y + x ] Using the relationship from the Pythagorean theorem for a right triangle formed: [ 3^2 = r^2 + y^2 \quad \text{which simplifies to} \quad 9 = r^2 + y^2 ]

3. Express volume of the cone

   The volume $V$ of the cone can be expressed using the formula for the volume of a cone: [ V = \frac{1}{3} \pi r^2 h ] We can substitute $h$ in terms of $y$ and $x$: [ V = \frac{1}{3} \pi r^2 (y + x) ]

4. Express $x$ in terms of $y$

   From the previous step, since $h = y + x$ and $y = 3 - x$, we can express $x$ in terms of $y$: [ x = 3 - y ]

5. Substitute and simplify the volume function

   Substitute the expressions for $h$ and $r$ into the volume equation: [ V = \frac{1}{3} \pi r^2 (y + (3 - y)) = \frac{1}{3} \pi r^2 \cdot 3 = \pi r^2 ] From $9 = r^2 + y^2$, we know $r^2 = 9 - y^2$. Substituting this into the volume, we can express $V$ only in terms of $y$: [ V(y) = \pi (9 - y^2) ]

6. Optimize the volume

   To find the maximum volume, we need to differentiate $V(y)$ with respect to $y$ and set the derivative equal to zero: [ V'(y) = \pi (-2y) = 0 \quad \Rightarrow \quad y = 0 ] This yields endpoints to check: ( y = 0 ) and ( y = 3 ).

7. Calculate the volume

   We will use the maximum found: At ( y = 3 ): [ V = \pi (9 - 3^2) = \pi (9 - 9) = 0 ] At ( y = 0 ): [ V = \pi (9 - 0) = 9\pi ]