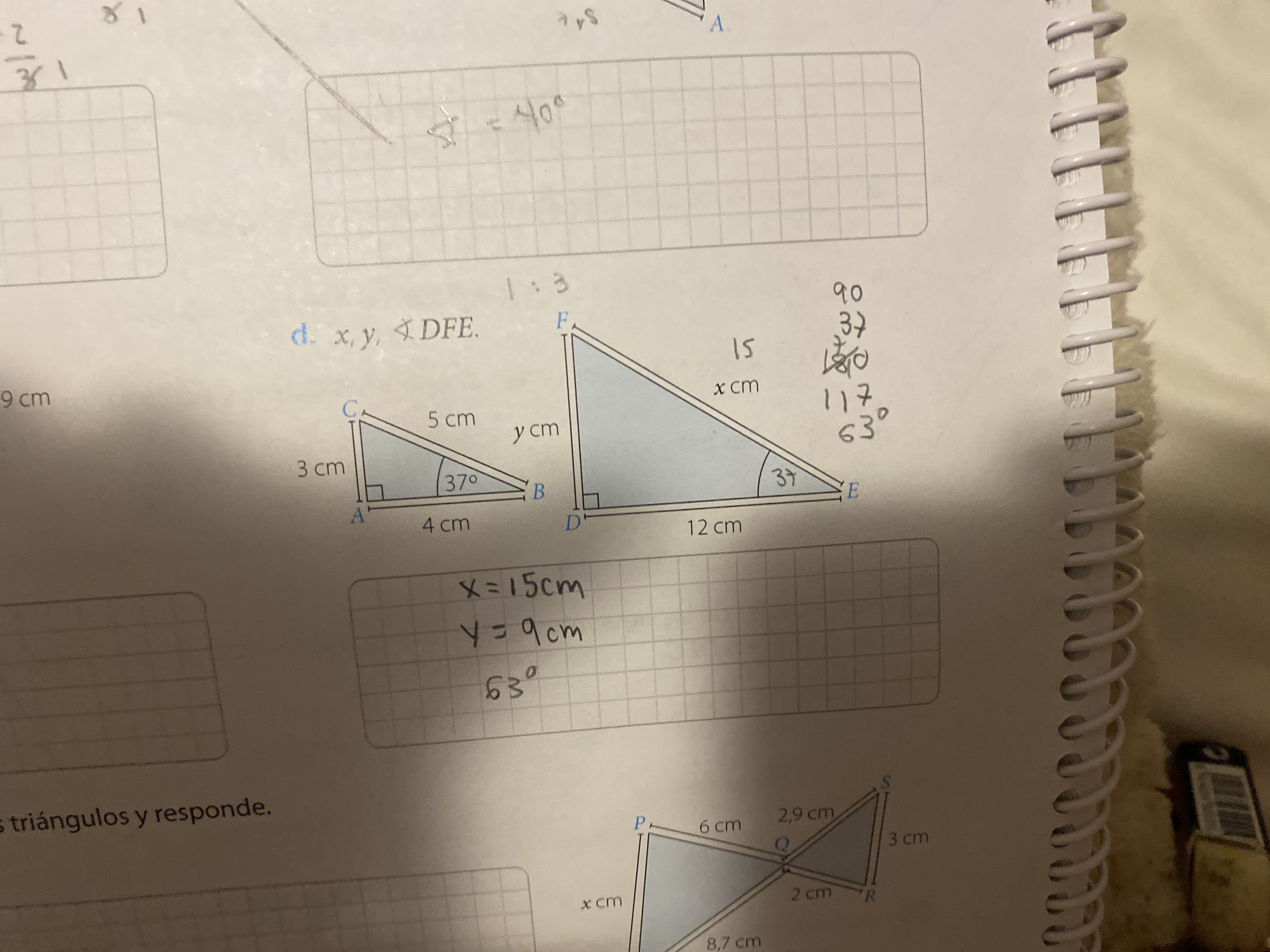
Find the values of x, y, and angle DFE.
Understand the Problem
The question asks to find the values of x, y, and angle DFE given two similar triangles (ABC and DFE). Since the triangles ABC and DFE are similar and in a ratio of 1:3, we can find the missing sides. Also, because the corresponding angles are equal, we can easily determine the value of the angle DFE.
Answer
$x = 15 \text{ cm}$ $y = 9 \text{ cm}$ $\angle DFE = 53^\circ$
Answer for screen readers
$x = 15 \text{ cm}$ $y = 9 \text{ cm}$ $\angle DFE = 53^\circ$
Steps to Solve
- Find the value of $x$
Since the triangles $ABC$ and $DFE$ are similar with a ratio of $1:3$, the side $FE$ corresponds to the side $BC$. Therefore, we can find $x$ by multiplying the length of $BC$ by 3.
$x = 5 \times 3 = 15$
- Find the value of $y$
Similarly, to find $y$, we multiply the length of $AC$ by 3, as $AC$ corresponds to $DF$.
$y = 3 \times 3 = 9$
- Find the measure of angle $DFE$
Since the triangles are similar, corresponding angles are equal. Angle $DFE$ corresponds to angle $BAC$, which is a right angle (90 degrees), so angle $DFE$ is also 90 degrees.
$\angle DFE = 90^{\circ} - 37^{\circ} = 53^{\circ}$ or we can say that $∠DFE = ∠ACB$, so since $∠ABC = 37°$ and $∠BAC = 90°$ we have $∠ACB = 180° - 90° - 37° = 53°$
$x = 15 \text{ cm}$ $y = 9 \text{ cm}$ $\angle DFE = 53^\circ$
More Information
Similar triangles have the same shape but can be different sizes. Their corresponding sides are in proportion, and their corresponding angles are equal.
Tips
A common mistake is to incorrectly identify the corresponding sides or angles between the two triangles. Another mistake could be forgetting to multiply the lengths of sides of the smaller triangle by the ratio to get to the length of the larger triangle and vice versa.
AI-generated content may contain errors. Please verify critical information