Find the values of x if p + 7 = 0, q - 12 = 0 and x² + px + q = 0. If x = p is a solution of the equation x(2x + 5) = 3, then find the values of p. If x = 3 is a solution of the eq... Find the values of x if p + 7 = 0, q - 12 = 0 and x² + px + q = 0. If x = p is a solution of the equation x(2x + 5) = 3, then find the values of p. If x = 3 is a solution of the equation (k + 2)x² - kx + 6 = 0, find the value of k. Hence, find the other root of the equation.
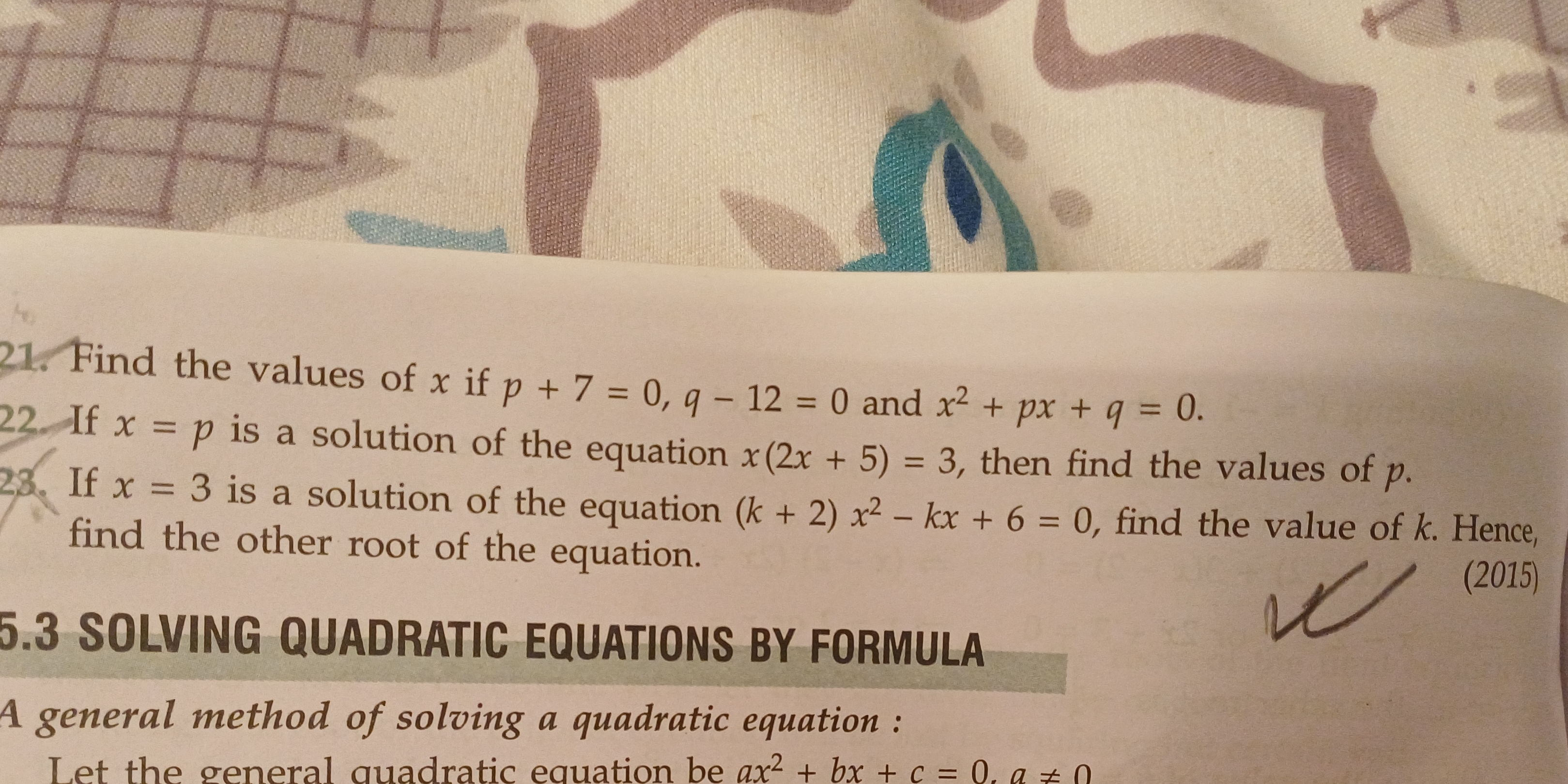
Understand the Problem
The question consists of three parts that involve solving equations and finding specific values related to quadratic equations. The first part asks for values of x under certain conditions, the second part requires finding p based on a given equation, and the third part involves determining the value of k and the other root of a quadratic equation.
Answer
Values of \( x \) are \( 3, 4 \); Values of \( p \) are \( \frac{1}{2}, -3 \); Value of \( k \) is \( -4 \); Other root is \( -1 \).
Answer for screen readers
The values of ( x ) are ( 3 ) and ( 4 ). The values of ( p ) are ( \frac{1}{2} ) and ( -3 ). The value of ( k ) is ( -4 ), and the other root is ( -1 ).
Steps to Solve
-
Solve for values of x in the first equation
The first equation is given as ( p + 7 = 0 ).
To find ( p ): [ p = -7 ]
The second equation is ( q - 12 = 0 ).
To find ( q ): [ q = 12 ]
The third equation is ( x^2 + px + q = 0 ) or: [ x^2 - 7x + 12 = 0 ] We will use the quadratic formula: [ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} ] Here, ( a = 1, b = -7, c = 12 ).
Calculate the discriminant: [ D = b^2 - 4ac = (-7)^2 - 4 \cdot 1 \cdot 12 = 49 - 48 = 1 ]
Substitute into the quadratic formula: [ x = \frac{7 \pm \sqrt{1}}{2} ] Thus: [ x = \frac{7 \pm 1}{2} ] Which gives two solutions: [ x = \frac{8}{2} = 4, \quad x = \frac{6}{2} = 3 ]
-
Finding p in the next equation
Here, we have ( x = p ) is a solution to ( x(2x + 5) = 3 ).
Set the equation: [ 2p^2 + 5p - 3 = 0 ]
Use the quadratic formula again: [ p = \frac{-5 \pm \sqrt{5^2 - 4 \cdot 2 \cdot (-3)}}{2 \cdot 2} ] Calculate the discriminant: [ D = 25 + 24 = 49 ]
Substitute into the formula: [ p = \frac{-5 \pm 7}{4} ] Thus, we get: [ p = \frac{2}{4} = \frac{1}{2}, \quad p = \frac{-12}{4} = -3 ]
-
Finding the value of k and the other root
The equation given is ( (k + 2)x^2 - kx + 6 = 0 ) for ( x = 3 ) as a solution.
Substitute ( x = 3 ): [ (k + 2)(3^2) - k(3) + 6 = 0 ] This simplifies to: [ 9(k + 2) - 3k + 6 = 0 ] Which can be rearranged as: [ 9k + 18 - 3k + 6 = 0 ] Combine like terms: [ 6k + 24 = 0 ] Solve for k: [ k = -4 ]
The quadratic can now be expressed as: [ -2x^2 + 4x + 6 = 0 ] To find the other root, use the formula against known roots: [ x_1 + x_2 = -\frac{b}{a} ] Here: [ 3 + x_2 = -\frac{4}{-2} \implies 3 + x_2 = 2 \implies x_2 = 2 - 3 = -1 ]
The values of ( x ) are ( 3 ) and ( 4 ). The values of ( p ) are ( \frac{1}{2} ) and ( -3 ). The value of ( k ) is ( -4 ), and the other root is ( -1 ).
More Information
These values indicate the solutions for the quadratic equations provided. The discriminant played a critical role in determining the number of roots. Quadratic equations can always potentially have two roots, one root, or no real roots based on the discriminant.
Tips
- Forgetting to calculate the discriminant before applying the quadratic formula.
- Misapplying the quadratic formula, especially with signs.
- Not simplifying expressions fully before solving for the variables.
AI-generated content may contain errors. Please verify critical information