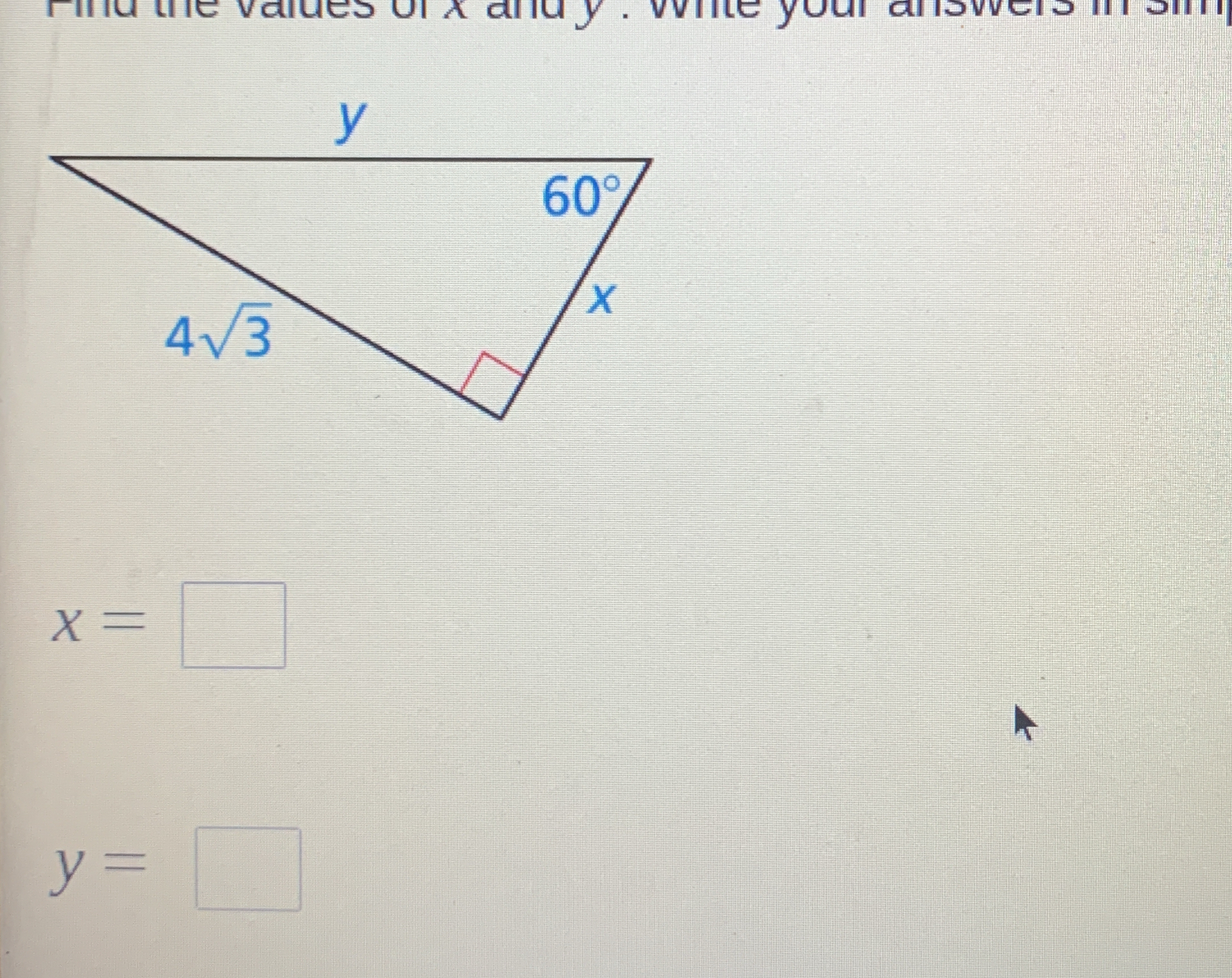
Find the values of x and y. Write your answers in simplified form.

Steps to Solve

1. Identify triangle components In the triangle, the known values are: the angle is $60^\circ$, the opposite side (to angle $60^\circ$) is $4\sqrt{3}$, and we need to find the adjacent side ($x$) and the hypotenuse ($y$).

2. Use tangent function for $x$ The tangent function relates the opposite side to the adjacent side: $$ \tan(60^\circ) = \frac{\text{opposite}}{\text{adjacent}} $$ Substituting in our known values: $$ \tan(60^\circ) = \frac{4\sqrt{3}}{x} $$ Since $\tan(60^\circ) = \sqrt{3}$, we have: $$ \sqrt{3} = \frac{4\sqrt{3}}{x} $$

3. Solve for $x$ Rearranging the equation for $x$ gives us: $$ x = \frac{4\sqrt{3}}{\sqrt{3}} $$ Simplifying this: $$ x = 4 $$

4. Use sine function for $y$ Now, we can use the sine function to find the hypotenuse: $$ \sin(60^\circ) = \frac{\text{opposite}}{\text{hypotenuse}} $$ Substituting in our known values: $$ \sin(60^\circ) = \frac{4\sqrt{3}}{y} $$ Since $\sin(60^\circ) = \frac{\sqrt{3}}{2}$, we have: $$ \frac{\sqrt{3}}{2} = \frac{4\sqrt{3}}{y} $$

5. Solve for $y$ Rearranging the equation for $y$ gives us: $$ y = \frac{4\sqrt{3}}{\frac{\sqrt{3}}{2}} $$ Multiplying by the reciprocal: $$ y = 4\sqrt{3} \cdot \frac{2}{\sqrt{3}} $$ Simplifying: $$ y = 8 $$