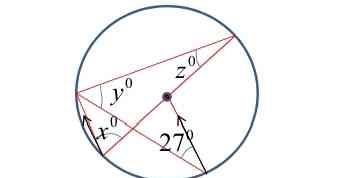
Find the values of angles x, y, and z in the given circle diagram.
Understand the Problem
The question requires us to find angles x, y, and z in a circle, given one angle of 27 degrees. By observing the diagram one can apply circle theorems to calculate these values.
Answer
$x = 27^\circ$ $y = 126^\circ$ $z = 54^\circ$
Answer for screen readers
$x = 27^\circ$ $y = 126^\circ$ $z = 54^\circ$
Steps to Solve
- Find the value of $x$
Angle $x$ is subtended by the same arc as the angle $27^\circ$. Therefore, $x = 27^\circ$.
- Find the value of $z$
Angle $z$ is the angle at the center subtended by the same arc that subtends the angle $x$ (or $27^\circ$) at the circumference. The angle at the center is twice the angle at the circumference. $$z = 2 \times 27^\circ = 54^\circ$$
- Find the value of $y$
The sum of angles in a quadrilateral inscribed in a circle is $180^\circ$. In our case, angle $y$ and the angle $z$ are opposite to each other. $$y + z = 180^\circ$$ $$y = 180^\circ - z = 180^\circ - 54^\circ = 126^\circ$$
$x = 27^\circ$ $y = 126^\circ$ $z = 54^\circ$
More Information
Circle theorems are used to find angles in circles. An inscribed quadrilateral is a quadrilateral whose vertices all lie on a circle. The opposite angles in an inscribed quadrilateral add up to $180^\circ$.
Tips
A common mistake is to confuse the angle at the center and the angle at the circumference subtended by the same arc. It is important to remember that the angle at the center is twice the angle at the circumference. Also, forgetting that opposite angles of a cyclic quadrilateral sum to $180^\circ$.
AI-generated content may contain errors. Please verify critical information