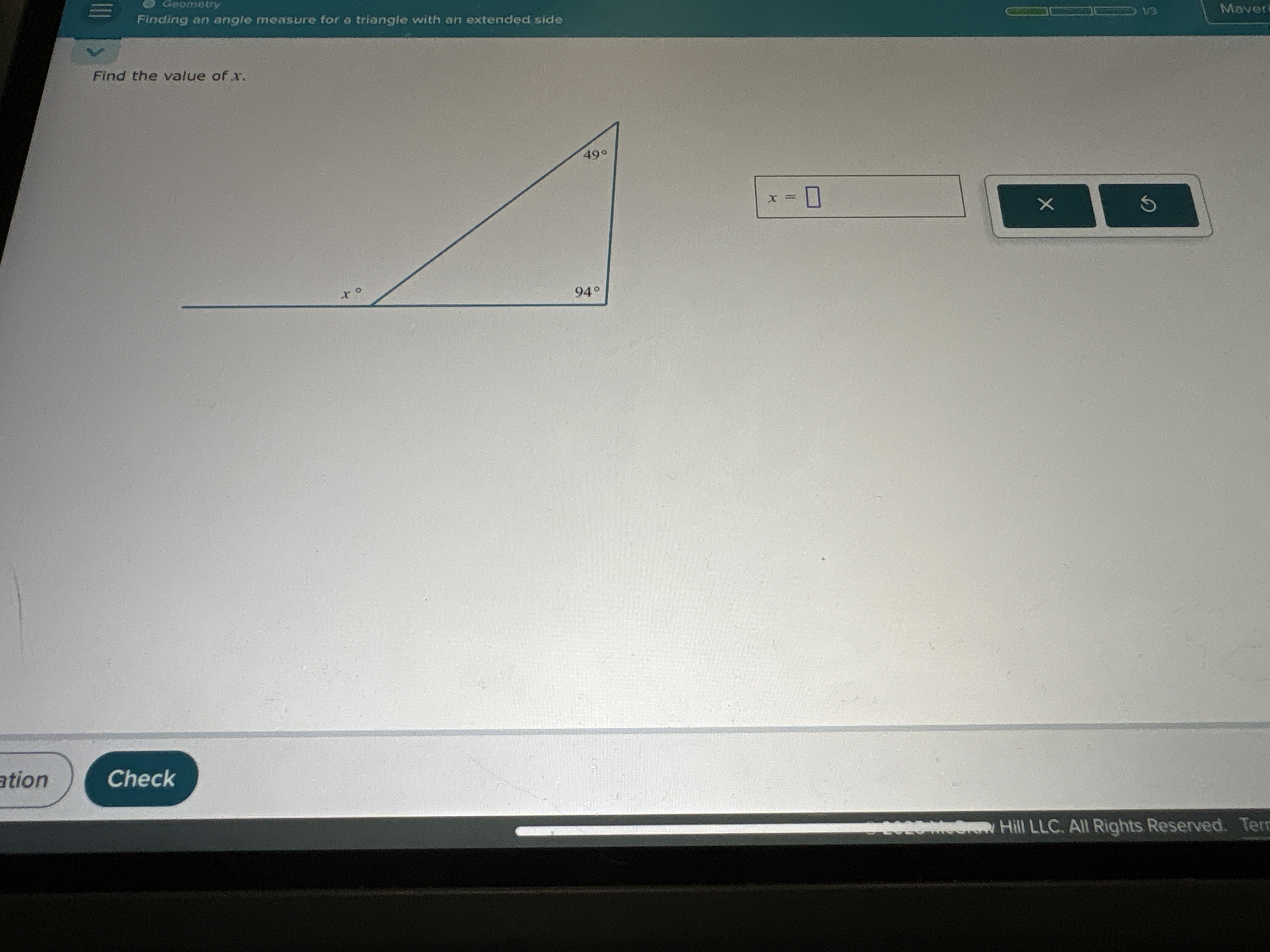
Find the value of x in the given triangle.
Understand the Problem
The question asks to find the value of the exterior angle 'x' of a triangle, given one interior angle (49°) and the adjacent angle to 'x' (94°). We can solve this by using the exterior angle theorem, which states that the measure of an exterior angle of a triangle is equal to the sum of the measures of the two non-adjacent interior angles.
Answer
$x = 135$
Answer for screen readers
$x = 135$
Steps to Solve
- Find the supplementary angle to the 94° angle
Since angles on a straight line add up to 180°, we can find the interior angle of the triangle adjacent to the $94^\circ$ angle. Let's call this angle $y$.
$$ y + 94^\circ = 180^\circ $$ $$ y = 180^\circ - 94^\circ = 86^\circ $$
- Use the triangle angle sum theorem
The angles in the triangle add up to 180°. Now we know two angles in the triangle, $49^\circ$ and $86^\circ$. We can find the third interior angle, which is supplementary to $x$. Let this third angle be $z$.
$$ z + 49^\circ + 86^\circ = 180^\circ $$ $$ z + 135^\circ = 180^\circ $$ $$ z = 180^\circ - 135^\circ = 45^\circ $$
- Find the value of x using supplementary angles
Since $x$ and $z$ are supplementary angles, they add up to 180°.
$$ x + z = 180^\circ $$ $$ x + 45^\circ = 180^\circ $$ $$ x = 180^\circ - 45^\circ = 135^\circ $$
$x = 135$
More Information
An exterior angle of a triangle is equal to the sum of the two non-adjacent interior angles, which is the Exterior Angle Theorem. In this case, $x = 49^\circ + 86^\circ = 135^\circ$.
Tips
A common mistake is to assume $x$ corresponds to the $94^\circ$ degree angle, by incorrectly assuming the triangle to be isosceles. Another common mistake is not recognizing that the angle adjacent to $x$ is supplementary, and incorrectly uses $94^\circ$ in calculations.
AI-generated content may contain errors. Please verify critical information