Find the value of $x$ in the following equation: $4^{2x+1} imes 5^{x-2} = 6^{1-x}$
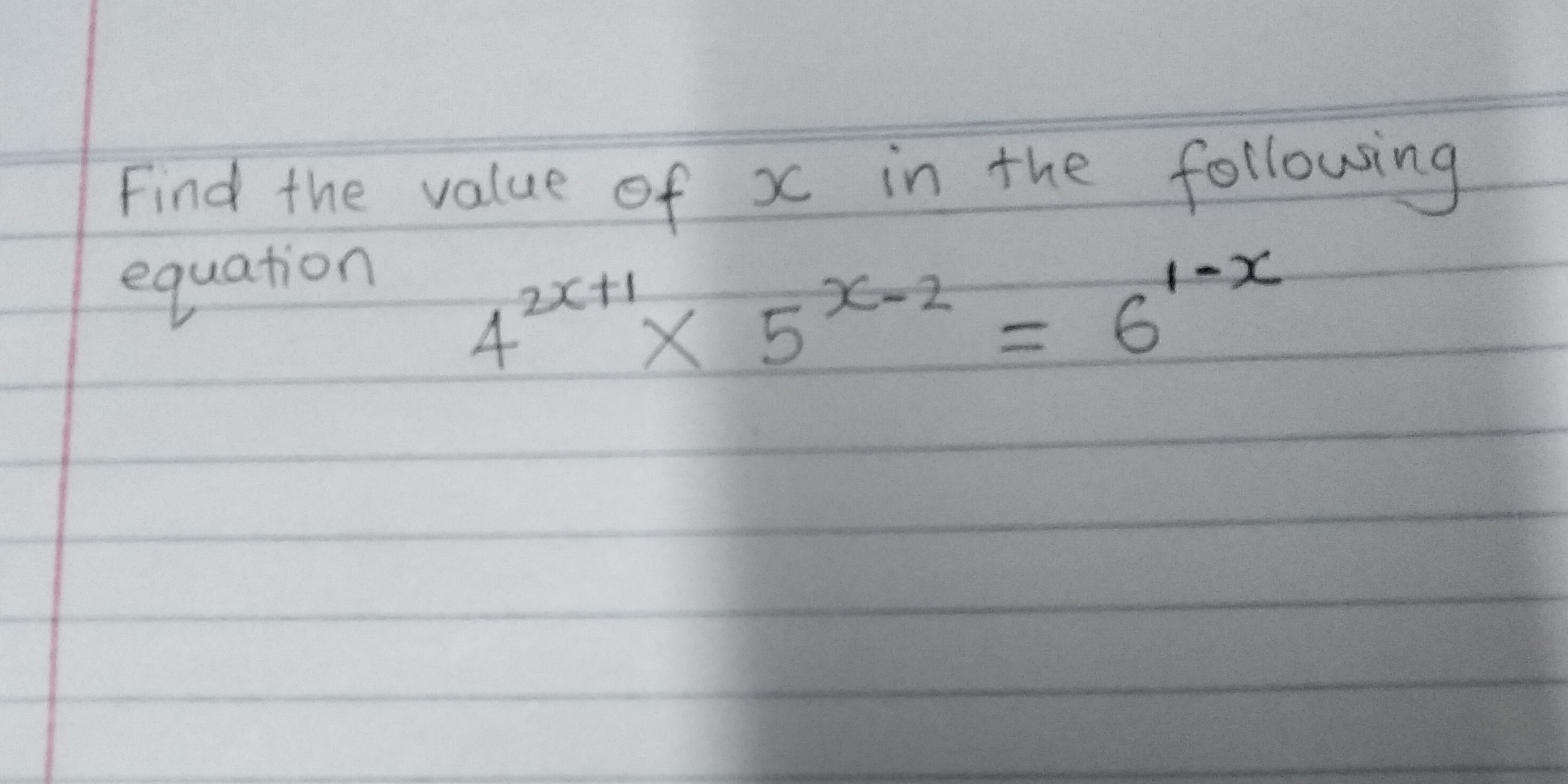
Understand the Problem
The question asks to find the value of $x$ in the equation $4^{2x+1} imes 5^{x-2} = 6^{1-x}$. This involves solving an exponential equation, which may require the use of logarithms or other algebraic manipulations to isolate and determine the value of $x$.
Answer
$x = \frac{\ln(\frac{75}{2})}{\ln(480)}$
Answer for screen readers
$x = \frac{\ln(\frac{75}{2})}{\ln(480)}$
$x \approx 0.5870$
Steps to Solve
-
Rewrite the equation The given equation is $4^{2x+1} \times 5^{x-2} = 6^{1-x}$.
-
Apply logarithms to both sides Take the natural logarithm (ln) of both sides of the equation: $$ \ln(4^{2x+1} \times 5^{x-2}) = \ln(6^{1-x}) $$
-
Use logarithm properties Apply the logarithm property $\ln(ab) = \ln(a) + \ln(b)$ on the left side and $\ln(a^b) = b\ln(a)$ on both sides: $$ \ln(4^{2x+1}) + \ln(5^{x-2}) = (1-x)\ln(6) $$ $$ (2x+1)\ln(4) + (x-2)\ln(5) = (1-x)\ln(6) $$
-
Expand the equation Expand each term: $$ 2x\ln(4) + \ln(4) + x\ln(5) - 2\ln(5) = \ln(6) - x\ln(6) $$
-
Group x terms Move all terms involving $x$ to the left side and constant terms to the right side: $$ 2x\ln(4) + x\ln(5) + x\ln(6) = \ln(6) - \ln(4) + 2\ln(5) $$
-
Factor out x Factor out $x$ from the left side: $$ x(2\ln(4) + \ln(5) + \ln(6)) = \ln(6) - \ln(4) + 2\ln(5) $$
-
Isolate x Divide both sides by $(2\ln(4) + \ln(5) + \ln(6))$ to solve for $x$: $$ x = \frac{\ln(6) - \ln(4) + 2\ln(5)}{2\ln(4) + \ln(5) + \ln(6)} $$
-
Simplify using logarithm properties Using the property $n\ln(a) = \ln(a^n)$, we have $2\ln(5) = \ln(5^2) = \ln(25)$ and $2\ln(4) = \ln(4^2) = \ln(16)$. $$ x = \frac{\ln(6) - \ln(4) + \ln(25)}{\ln(16) + \ln(5) + \ln(6)} $$
-
Further simplification Using the property $\ln(a) + \ln(b) = \ln(ab)$ and $\ln(a) - \ln(b) = \ln(\frac{a}{b})$, we can simplify further: $$ x = \frac{\ln(\frac{6 \times 25}{4})}{\ln(16 \times 5 \times 6)} = \frac{\ln(\frac{150}{4})}{\ln(480)} = \frac{\ln(\frac{75}{2})}{\ln(480)} $$
-
Approximate the value of x $$ x = \frac{\ln(37.5)}{\ln(480)} \approx \frac{3.6243}{6.1738} \approx 0.5870 $$
$x = \frac{\ln(\frac{75}{2})}{\ln(480)}$
$x \approx 0.5870$
More Information
The solution to the equation $4^{2x+1} \times 5^{x-2} = 6^{1-x}$ is approximately $0.5870$. This value was obtained by taking the natural logarithm of both sides of the equation, applying logarithm properties, and then isolating $x$.
Tips
A common mistake is to incorrectly apply logarithm properties, particularly when dealing with sums and products within the logarithm. Another common mistake is computational errors when evaluating the logarithms using a calculator.
AI-generated content may contain errors. Please verify critical information