Find the value of sin(150).
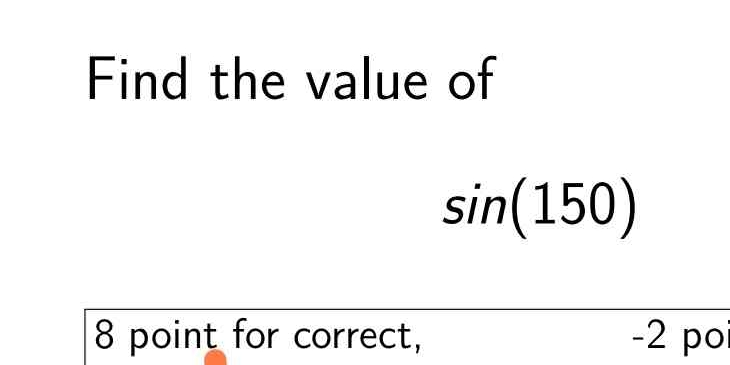
Understand the Problem
The question is asking to find the value of the sine of 150 degrees, which is a trigonometry problem. To solve this, we need to find the sine of 150 degrees.
Answer
$\frac{1}{2}$
Answer for screen readers
$\frac{1}{2}$
Steps to Solve
- Express 150 degrees as a reference angle.
$150^\circ$ can be expressed as $180^\circ - 30^\circ$. This helps us relate the sine of $150^\circ$ to the sine of its reference angle, $30^\circ$. 2. Use the property $sin(180^\circ - \theta) = sin(\theta)$
The sine of an angle in the second quadrant (like $150^\circ$) is positive. Therefore, $sin(150^\circ) = sin(180^\circ - 30^\circ) = sin(30^\circ)$. 3. Find the value of $sin(30^\circ)$
$sin(30^\circ)$ is a standard trigonometric value, which is equal to $\frac{1}{2}$.
$\frac{1}{2}$
More Information
The sine function gives the y-coordinate of a point on the unit circle. At 150 degrees, the y-coordinate is the same as the y-coordinate at 30 degrees, which is $\frac{1}{2}$.
Tips
A common mistake is to confuse the sine and cosine or to forget the sign of the trigonometric function in the correct quadrant. Since 150 degrees is in the second quadrant, sine is positive.
AI-generated content may contain errors. Please verify critical information