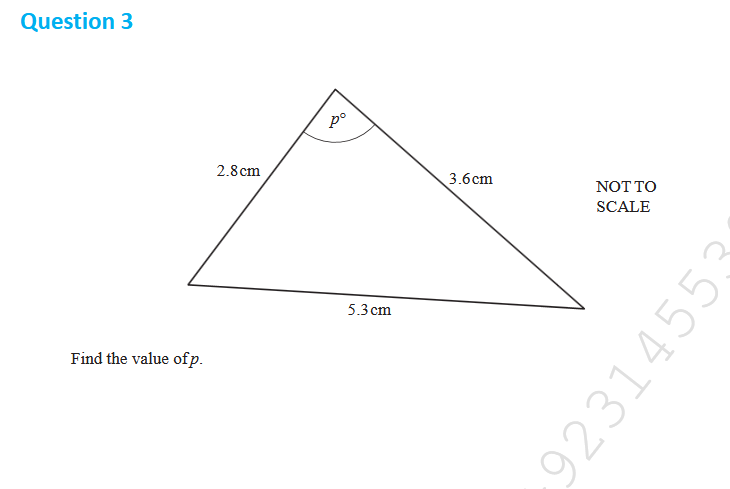
Find the value of p.

Steps to Solve

1. State the Law of Cosines To find the angle ( p ) in triangle given the side lengths, we can use the Law of Cosines, which states: $$ c^2 = a^2 + b^2 - 2ab \cos(p) $$ Here, ( c ) is the side opposite angle ( p ).

2. Identify the sides In this case, let:

• ( a = 2.8 , \text{cm} )
• ( b = 3.6 , \text{cm} )
• ( c = 5.3 , \text{cm} )

Plugging these values into the Law of Cosines equation, we have: $$ 5.3^2 = 2.8^2 + 3.6^2 - 2 \cdot 2.8 \cdot 3.6 \cdot \cos(p) $$

3. Calculate the squares of the sides Compute ( a^2 ), ( b^2 ), and ( c^2 ): $$ 5.3^2 = 28.09 $$ $$ 2.8^2 = 7.84 $$ $$ 3.6^2 = 12.96 $$

4. Insert values into the equation Now substitute the squares back into the equation: $$ 28.09 = 7.84 + 12.96 - 2 \cdot 2.8 \cdot 3.6 \cdot \cos(p) $$

5. Simplify the equation Combine the terms: $$ 28.09 = 20.8 - 20.16 \cos(p) $$

6. Rearranging for ( \cos(p) ) Rearranging gives: $$ 20.16 \cos(p) = 20.8 - 28.09 $$ $$ 20.16 \cos(p) = -7.29 $$

7. Calculate ( \cos(p) ) Now solve for ( \cos(p) ): $$ \cos(p) = \frac{-7.29}{20.16} $$ Calculate the value: $$ \cos(p) \approx -0.362 $$

8. Find angle ( p ) Finally, use the inverse cosine to find ( p ): $$ p = \cos^{-1}(-0.362) $$

9. Calculate the angle Using a calculator: $$ p \approx 111.5^\circ $$