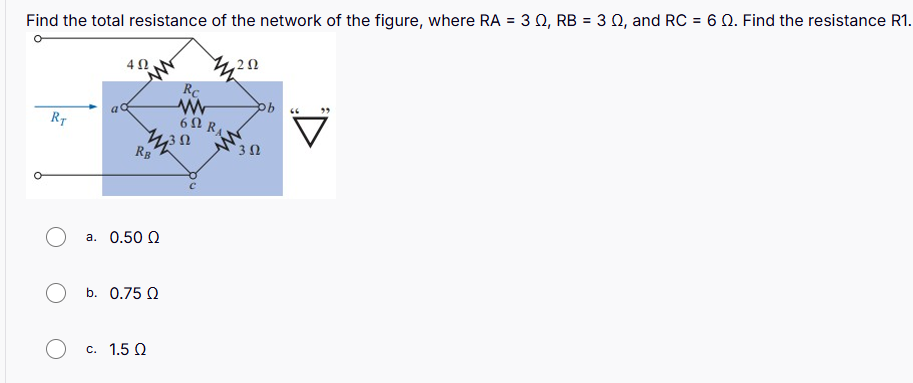
Find the total resistance of the network of the figure, where RA = 3 Ω, RB = 3 Ω, and RC = 6 Ω. Find the resistance R1.

Steps to Solve

1. Identify resistor combinations
   The resistors in the circuit include ( R_A = 3 , \Omega ), ( R_B = 3 , \Omega ), and ( R_C = 6 , \Omega ). We need to analyze how these resistors are connected (series or parallel).

2. Calculate equivalent resistances for R_B and R_C
   Resistors ( R_B ) (3 Ω) and ( R_C ) (6 Ω) are in parallel. The formula for equivalent resistance ( R_{eq} ) for resistors in parallel is given by:
   $$ \frac{1}{R_{eq}} = \frac{1}{R_B} + \frac{1}{R_C} $$
   Substituting the values:
   $$ \frac{1}{R_{eq}} = \frac{1}{3} + \frac{1}{6} $$
   Finding a common denominator (6):
   $$ \frac{1}{R_{eq}} = \frac{2}{6} + \frac{1}{6} = \frac{3}{6} = \frac{1}{2} $$
   Thus,
   $$ R_{eq} = 2 , \Omega $$

3. Combine R_A and R_eq in series
   Now, ( R_A ) (3 Ω) is in series with ( R_{eq} ) (2 Ω):
   The total resistance ( R_T ) is:
   $$ R_T = R_A + R_{eq} = 3 + 2 = 5 , \Omega $$

4. Final Total Resistance
   The total resistance of the network is ( R_T = 5 , \Omega ).