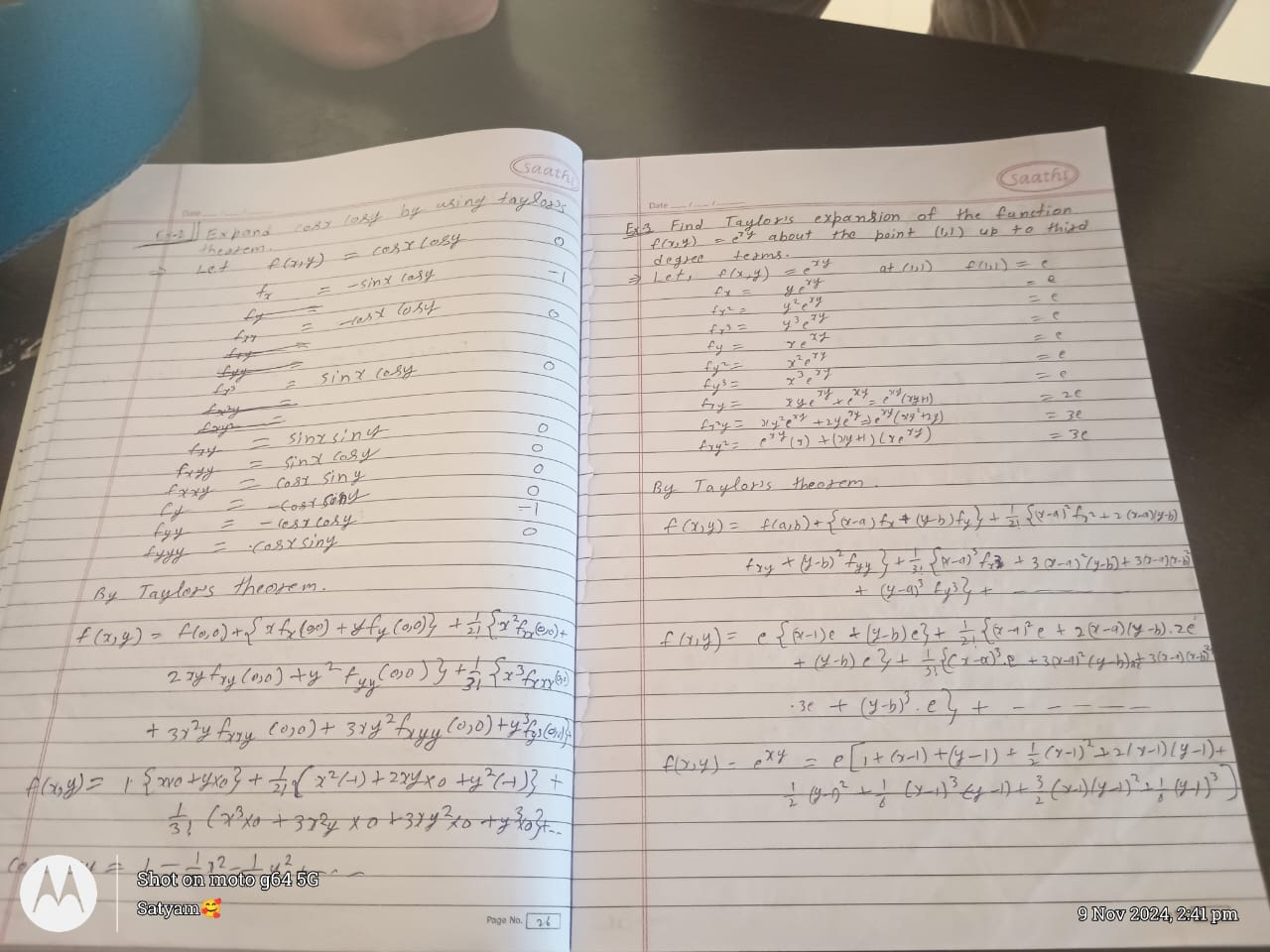
Find the Taylor series expansion of the function f(x,y) = e^(xy) about the point (1,1) up to third degree terms.
Understand the Problem
The question involves finding the Taylor series expansion of the function f(x,y) = e^(xy) around the point (1,1) up to third-degree terms, using Taylor's theorem. It seeks assistance in deriving the formula and the expansion step-by-step.
Answer
The Taylor series expansion of \( f(x, y) = e^{xy} \) around \( (1, 1) \) to third degree is: $$ f(x, y) = e + e(x - 1) + e(y - 1) + \frac{e}{2}(x - 1)^2 + 2e(x - 1)(y - 1) + \frac{e}{2}(y - 1)^2 + \frac{e}{6}(x - 1)^3 + \frac{3e}{2}(x - 1)^2(y - 1) + \frac{3e}{2}(x - 1)(y - 1)^2 + \frac{e}{6}(y - 1)^3 $$
Answer for screen readers
The Taylor series expansion of ( f(x, y) = e^{xy} ) around the point ( (1, 1) ) up to third-degree terms is:
$$ f(x, y) = e + e(x - 1) + e(y - 1) + \frac{e}{2}(x - 1)^2 + 2e(x - 1)(y - 1) + \frac{e}{2}(y - 1)^2 + \frac{e}{6}(x - 1)^3 + \frac{3e}{2}(x - 1)^2(y - 1) + \frac{3e}{2}(x - 1)(y - 1)^2 + \frac{e}{6}(y - 1)^3 $$
Steps to Solve
- Identify the function and the point of expansion
We start with the function ( f(x, y) = e^{xy} ) and we want to expand it around the point ( (1, 1) ).
- Calculate the function value at the expansion point
Find ( f(1, 1) ):
$$ f(1, 1) = e^{1 \cdot 1} = e $$
- Calculate the first-order partial derivatives
Compute the first-order partial derivatives at ( (1, 1) ):
- ( f_x(x, y) = ye^{xy} )
- ( f_y(x, y) = xe^{xy} )
Evaluating at ( (1, 1) ):
- ( f_x(1, 1) = 1 \cdot e = e )
- ( f_y(1, 1) = 1 \cdot e = e )
- Calculate the second-order partial derivatives
Compute the second-order partial derivatives:
- ( f_{xx}(x, y) = y^2 e^{xy} )
- ( f_{yy}(x, y) = x^2 e^{xy} )
- ( f_{xy}(x, y) = e^{xy} + xy e^{xy} )
Evaluating at ( (1, 1) ):
- ( f_{xx}(1, 1) = e )
- ( f_{yy}(1, 1) = e )
- ( f_{xy}(1, 1) = e + e = 2e )
- Calculate the third-order partial derivatives
Compute the third-order partial derivatives:
- ( f_{xxx}(x, y) = y^3 e^{xy} )
- ( f_{yyy}(x, y) = x^3 e^{xy} )
- ( f_{xxy}(x, y) = 2y e^{xy} + xy^2 e^{xy} )
- ( f_{xyy}(x, y) = 2x e^{xy} + x^2 ye^{xy} )
Evaluating at ( (1, 1) ):
- ( f_{xxx}(1, 1) = e )
- ( f_{yyy}(1, 1) = e )
- ( f_{xxy}(1, 1) = 2e + e = 3e )
- ( f_{xyy}(1, 1) = 2e + e = 3e )
- Use Taylor's theorem to construct the series expansion
The Taylor series expansion is given by:
$$ f(x, y) = f(1, 1) + f_x(1, 1)(x-1) + f_y(1, 1)(y-1) + \frac{1}{2!} \left[ f_{xx}(1, 1)(x-1)^2 + 2f_{xy}(1, 1)(x-1)(y-1) + f_{yy}(1, 1)(y-1)^2 \right] + \frac{1}{3!} \left[ f_{xxx}(1, 1)(x-1)^3 + 3f_{xxy}(1, 1)(x-1)^2(y-1) + 3f_{xyy}(1, 1)(x-1)(y-1)^2 + f_{yyy}(1, 1)(y-1)^3 \right] $$
- Simplify the expansion
Substitute the computed values into the Taylor series expansion:
$$ f(x, y) = e + e(x-1) + e(y-1) + \frac{1}{2} \left[ e(x-1)^2 + 2(2e)(x-1)(y-1) + e(y-1)^2 \right] + \frac{1}{6} \left[ e(x-1)^3 + 3(3e)(x-1)^2(y-1) + 3(3e)(x-1)(y-1)^2 + e(y-1)^3 \right] $$
This expands to a third-degree polynomial in ( (x-1) ) and ( (y-1) ).
The Taylor series expansion of ( f(x, y) = e^{xy} ) around the point ( (1, 1) ) up to third-degree terms is:
$$ f(x, y) = e + e(x - 1) + e(y - 1) + \frac{e}{2}(x - 1)^2 + 2e(x - 1)(y - 1) + \frac{e}{2}(y - 1)^2 + \frac{e}{6}(x - 1)^3 + \frac{3e}{2}(x - 1)^2(y - 1) + \frac{3e}{2}(x - 1)(y - 1)^2 + \frac{e}{6}(y - 1)^3 $$
More Information
The Taylor series is a powerful tool in mathematics for approximating functions. This expansion allows us to evaluate the function ( e^{xy} ) near the point ( (1, 1) ) using polynomial approximation.
Tips
- Forgetting to account for higher-order derivatives.
- Not correctly applying the factorial in Taylor series terms.
- Miscalculating the derivatives at the point of expansion.
AI-generated content may contain errors. Please verify critical information