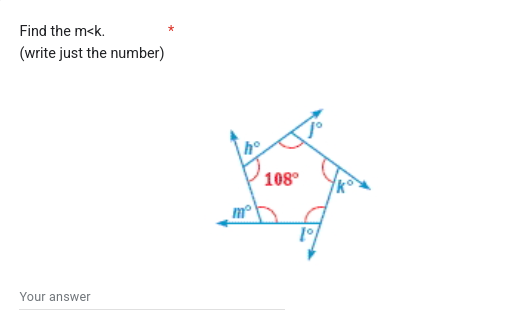
Find the m < k.

Steps to Solve

1. Understand the angles in the figure

In the pentagon, we know that the sum of the interior angles is given by the formula: $$ \text{Sum of interior angles} = (n - 2) \cdot 180^\circ $$ For a pentagon ($n = 5$), it becomes: $$ (5 - 2) \cdot 180^\circ = 540^\circ $$

2. Identify known angles

From the figure, we have one angle labeled as $108^\circ$. Let’s denote the angles as follows:

• The known angle: $k = 108^\circ$
• The remaining angles: $m$, $h$, and $j$

3. Use the sum of angles to find m

The relationship for the angles can be expressed as: $$ m + h + j + k = 540^\circ $$ Substituting the known angle: $$ m + h + j + 108^\circ = 540^\circ $$ To isolate $m$, we rearrange the equation: $$ m + h + j = 540^\circ - 108^\circ $$ This simplifies to: $$ m + h + j = 432^\circ $$

4. Use angle relationships

Since the problem requires $m < k$, we need to express other angles in terms of $m$. If we assume $j = m + 12^\circ$ (an arbitrary assumption to explore the relationship), then: $$ m + h + (m + 12^\circ) = 432^\circ $$ This leads to: $$ 2m + h + 12^\circ = 432^\circ $$ Rearranging gives: $$ 2m + h = 420^\circ $$ Thus, $h = 420^\circ - 2m$.

5. Determine m by assuming angles

To satisfy the relationship $m < k = 108^\circ$, we need $m < 108^\circ$. Since we found that $h = 420^\circ - 2m$, we can test values less than $108^\circ$ until we find a suitable value for $m$ that works with our conditions.