Find the limit: lim (x->1) (x^(1/6) - 1) / (x - 1)
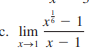
Understand the Problem
The question asks us to find the limit of the function (x^(1/6) - 1) / (x - 1) as x approaches 1. This is a calculus problem involving limits.
Answer
$\frac{1}{6}$
Answer for screen readers
$\frac{1}{6}$
Steps to Solve
-
Recognize the limit as a derivative
The given limit has the form of the definition of a derivative. Recall that the derivative of a function $f(x)$ at a point $a$ is defined as:
$f'(a) = \lim_{x \to a} \frac{f(x) - f(a)}{x - a}$
-
Identify the function and the point
Comparing the given limit $\lim_{x \to 1} \frac{x^{\frac{1}{6}} - 1}{x - 1}$ with the definition of the derivative, we can identify $f(x) = x^{\frac{1}{6}}$ and $a = 1$. Thus, we need to find $f'(1)$.
-
Find the derivative of the function
Differentiate $f(x) = x^{\frac{1}{6}}$ with respect to $x$ using the power rule:
$f'(x) = \frac{1}{6}x^{\frac{1}{6} - 1} = \frac{1}{6}x^{-\frac{5}{6}}$
-
Evaluate the derivative at the point
Evaluate $f'(x)$ at $x = 1$: $f'(1) = \frac{1}{6}(1)^{-\frac{5}{6}} = \frac{1}{6}(1) = \frac{1}{6}$
$\frac{1}{6}$
More Information
The limit represents the derivative of the function $f(x) = x^{\frac{1}{6}}$ evaluated at $x = 1$. This provides a direct method for solving limits of this form by relating them back to derivatives.
Tips
A common mistake is attempting to directly substitute $x = 1$ into the expression, which results in an indeterminate form $\frac{0}{0}$. L'Hopital's rule could be used, but recognizing the limit as a derivative makes the solution more straightforward.
AI-generated content may contain errors. Please verify critical information