Find the limit: lim (x->0) (1 - √(cosx)) / (2x²)
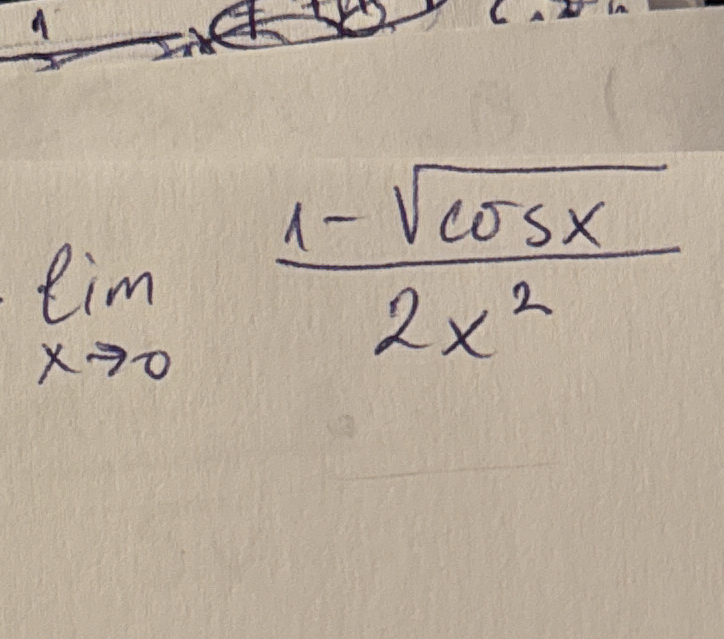
Understand the Problem
The question asks to find the limit of the function (1 - √(cosx)) / (2x²) as x approaches 0. This problem likely involves techniques for evaluating limits, such as L'Hôpital's Rule or trigonometric identities, since direct substitution results in an indeterminate form.
Answer
$\frac{1}{8}$
Answer for screen readers
$\frac{1}{8}$
Steps to Solve
- Multiply by the conjugate Multiply both the numerator and denominator by the conjugate of the numerator, which is $1 + \sqrt{\cos x}$.
$$ \lim_{x \to 0} \frac{1 - \sqrt{\cos x}}{2x^2} \cdot \frac{1 + \sqrt{\cos x}}{1 + \sqrt{\cos x}} = \lim_{x \to 0} \frac{1 - \cos x}{2x^2(1 + \sqrt{\cos x})} $$
- Use the trigonometric identity $1 - \cos x = 2\sin^2(x/2)$
$$ \lim_{x \to 0} \frac{2\sin^2(x/2)}{2x^2(1 + \sqrt{\cos x})} = \lim_{x \to 0} \frac{\sin^2(x/2)}{x^2(1 + \sqrt{\cos x})} $$
- Rewrite the expression Rewrite the $x^2$ term as $4(x/2)^2$ in the denominator:
$$ \lim_{x \to 0} \frac{\sin^2(x/2)}{4(x/2)^2(1 + \sqrt{\cos x})} = \lim_{x \to 0} \frac{1}{4(1 + \sqrt{\cos x})} \cdot \frac{\sin^2(x/2)}{(x/2)^2} $$
-
Apply the limit $\lim_{u \to 0} \frac{\sin u}{u} = 1$ Since $\lim_{x \to 0} \frac{\sin(x/2)}{x/2} = 1$, we have $\lim_{x \to 0} \frac{\sin^2(x/2)}{(x/2)^2} = 1$.
-
Evaluate the remaining limit
$$ \lim_{x \to 0} \frac{1}{4(1 + \sqrt{\cos x})} \cdot 1 = \frac{1}{4(1 + \sqrt{\cos 0})} = \frac{1}{4(1 + \sqrt{1})} = \frac{1}{4(1 + 1)} = \frac{1}{4(2)} = \frac{1}{8} $$
$\frac{1}{8}$
More Information
The limit of the given function as $x$ approaches 0 is $\frac{1}{8}$.
Tips
A common mistake to avoid is incorrectly applying L'Hôpital's Rule or trigonometric identities. Also, not multiplying by the conjugate can make the problem more complex. Another common mistake is an error in the algebra.
AI-generated content may contain errors. Please verify critical information