Find the inverse of the matrix A = [[1, 1, 2], [1, 2, 3], [2, 3, 1]] by Gauss-elimination method.
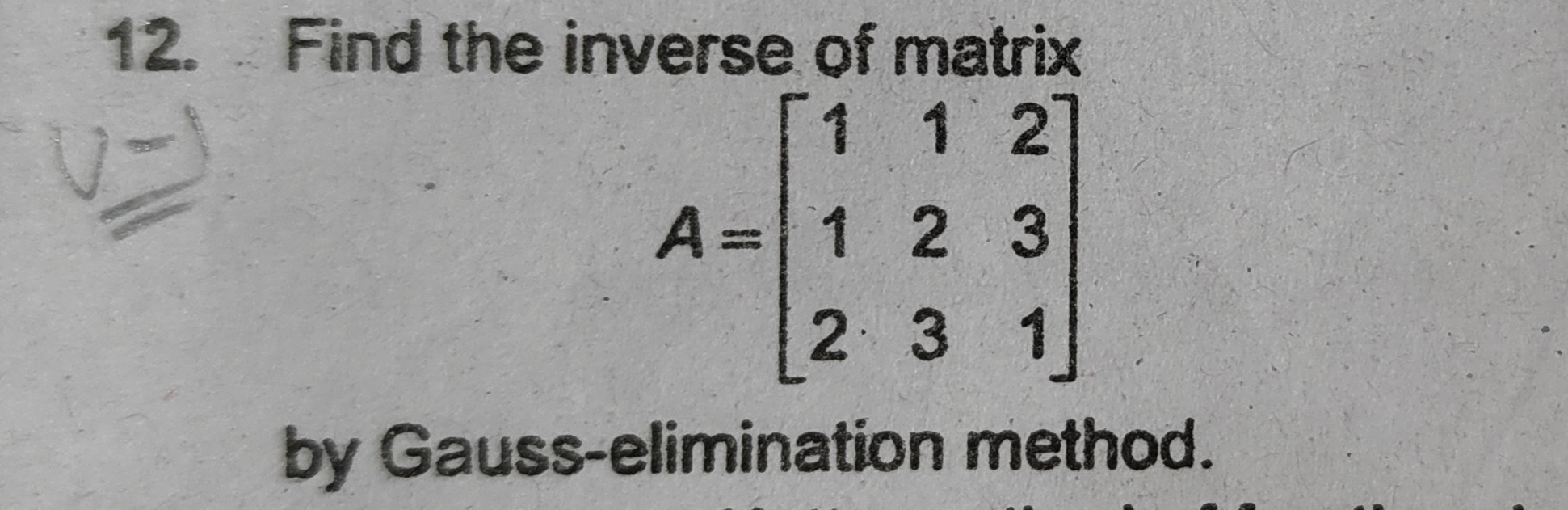
Understand the Problem
The question is asking to find the inverse of a given matrix using the Gauss-elimination method. This involves performing row operations to transform the matrix into its inverse form.
Answer
The inverse of matrix \( A \) is $$ A^{-1} = \begin{bmatrix} 1 & -1 & 1 \\ -1 & 1 & 1 \\ \frac{1}{4} & \frac{1}{4} & -\frac{1}{4} \end{bmatrix} $$
Answer for screen readers
The inverse of matrix ( A ) is given by
$$ A^{-1} = \begin{bmatrix} 1 & -1 & 1 \ -1 & 1 & 1 \ \frac{1}{4} & \frac{1}{4} & -\frac{1}{4} \end{bmatrix} $$
Steps to Solve
-
Setup the augmented matrix
To find the inverse of matrix ( A ), we start by creating an augmented matrix that combines ( A ) with the identity matrix:
$$ \begin{bmatrix} 1 & 1 & 2 & | & 1 & 0 & 0 \ 1 & 2 & 3 & | & 0 & 1 & 0 \ 2 & 3 & 1 & | & 0 & 0 & 1 \end{bmatrix} $$
-
Perform row operations to reach Row Echelon Form (REF)
We need to use row operations to transform the left side of the augmented matrix into the identity matrix. Begin by making the first column below the leading 1 into zeros:
- Subtract Row 1 from Row 2
- Subtract ( 2 \times \text{Row 1} ) from Row 3
This results in:
$$ \begin{bmatrix} 1 & 1 & 2 & | & 1 & 0 & 0 \ 0 & 1 & 1 & | & -1 & 1 & 0 \ 0 & 1 & -3 & | & -2 & 0 & 1 \end{bmatrix} $$
-
Continue row operations to make leading 1's and zeros
Next, make Row 2's leading coefficient the only non-zero value in its column:
- Subtract Row 2 from Row 3
Thus, we have:
$$ \begin{bmatrix} 1 & 1 & 2 & | & 1 & 0 & 0 \ 0 & 1 & 1 & | & -1 & 1 & 0 \ 0 & 0 & -4 & | & -1 & -1 & 1 \end{bmatrix} $$
-
Make leading coefficients 1
Divide Row 3 by -4 to make the leading coefficient 1:
$$ \begin{bmatrix} 1 & 1 & 2 & | & 1 & 0 & 0 \ 0 & 1 & 1 & | & -1 & 1 & 0 \ 0 & 0 & 1 & | & \frac{1}{4} & \frac{1}{4} & -\frac{1}{4} \end{bmatrix} $$
-
Back substitution to get the identity matrix
Now we perform back-substitution to turn the left side into the identity matrix:
- Replace Row 2 with ( \text{Row 2} - \text{Row 3} )
- Replace Row 1 with ( \text{Row 1} - 2 \times \text{Row 3} )
These operations lead to:
$$ \begin{bmatrix} 1 & 1 & 0 & | & \frac{1}{2} & -\frac{1}{2} & \frac{1}{2} \ 0 & 1 & 0 & | & -\frac{1}{2} & \frac{1}{2} & \frac{1}{2} \ 0 & 0 & 1 & | & \frac{1}{4} & \frac{1}{4} & -\frac{1}{4} \end{bmatrix} $$
Finally, subtract Row 2 from Row 1 to eliminate the remaining non-zero entries above the leading 1 of Row 2:
$$ \begin{bmatrix} 1 & 0 & 0 & | & 1 & -1 & 1 \ 0 & 1 & 0 & | & -1 & 1 & 1 \ 0 & 0 & 1 & | & \frac{1}{4} & \frac{1}{4} & -\frac{1}{4} \end{bmatrix} $$
-
Identify the inverse matrix
The right-hand side of the augmented matrix is the inverse of ( A ):
$$ A^{-1} = \begin{bmatrix} 1 & -1 & 1 \ -1 & 1 & 1 \ \frac{1}{4} & \frac{1}{4} & -\frac{1}{4} \end{bmatrix} $$
The inverse of matrix ( A ) is given by
$$ A^{-1} = \begin{bmatrix} 1 & -1 & 1 \ -1 & 1 & 1 \ \frac{1}{4} & \frac{1}{4} & -\frac{1}{4} \end{bmatrix} $$
More Information
The process of finding the inverse of a matrix using the Gauss-elimination method involves transforming the matrix into the identity form through systematic row operations. The resulting matrix on the right of the augmented matrix will be the inverse.
Tips
- Ignoring the row operations: It's crucial to apply row operations systematically. Failing to do so can lead to incorrect results.
- Not checking the final result: Always multiply the original matrix by its supposed inverse to verify if the result is indeed the identity matrix.
- Focusing only on the left-hand side: Ensure to also keep track of changes in the identity matrix on the right side.
AI-generated content may contain errors. Please verify critical information