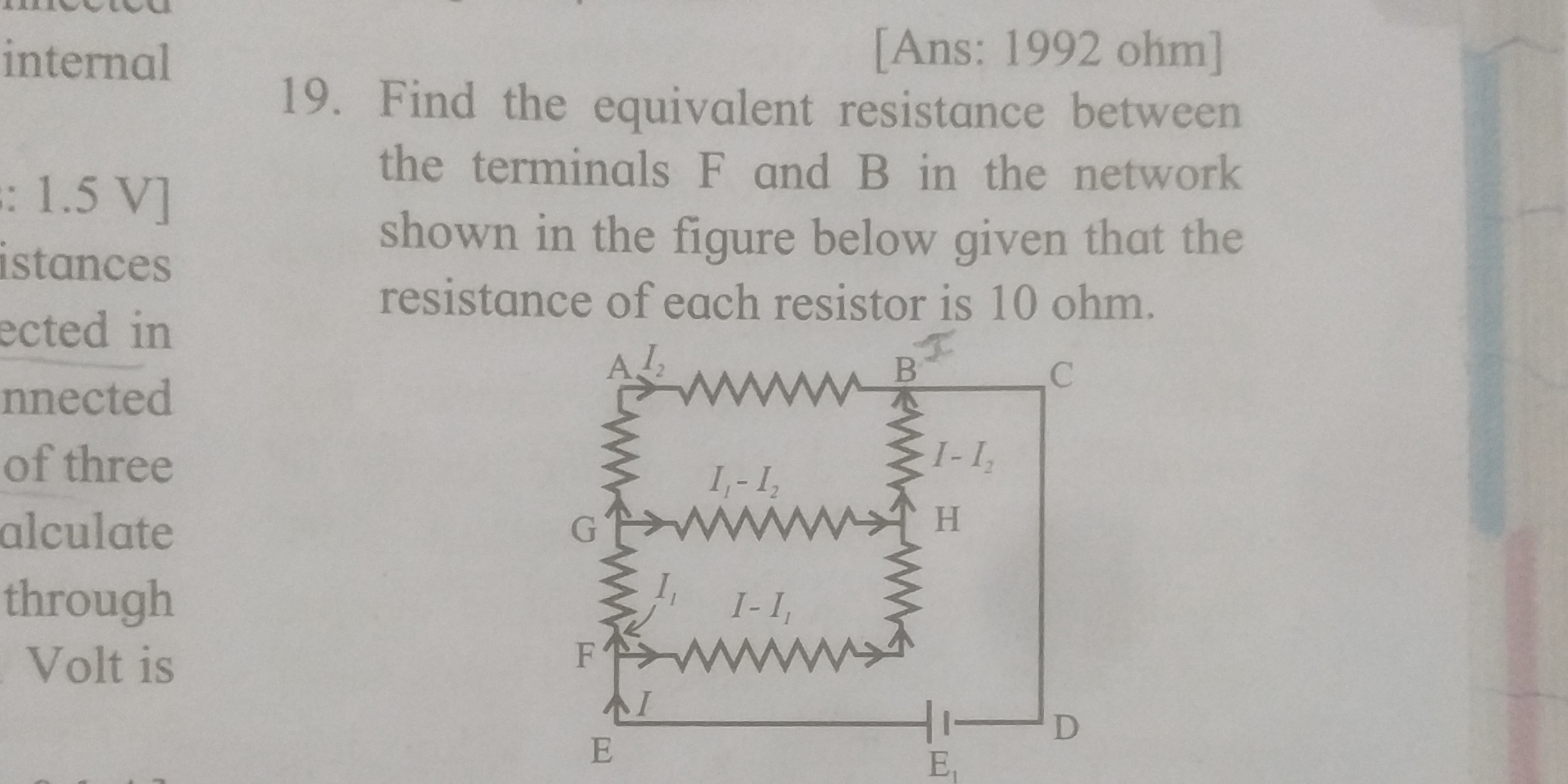
Find the equivalent resistance between the terminals F and B in the network shown in the figure below given that the resistance of each resistor is 10 ohm.
Understand the Problem
The question is asking to find the equivalent resistance between two terminals, F and B, in a resistor network, given that each resistor has a resistance of 10 ohms. This requires understanding of series and parallel resistor combinations.
Answer
The equivalent resistance is $1992 \, \Omega$.
Answer for screen readers
The equivalent resistance between terminals F and B is $R_{eq} = 1992 , \Omega$.
Steps to Solve
- Identify the resistors and connections
In the circuit, each resistor has a resistance of 10 ohms. Identify how they are connected.
- Group resistors in series and parallel
Notice that there are groups of resistors in parallel and in series. For resistors in series, the total resistance $R_s$ is given by: $$ R_s = R_1 + R_2 $$
For resistors in parallel, the total resistance $R_p$ is calculated as: $$ \frac{1}{R_p} = \frac{1}{R_1} + \frac{1}{R_2} $$
- Calculate equivalent resistances step by step
- Identify the resistors in parallel between terminals F and B, which includes multiple parallel combinations. Calculate the equivalent resistance for these groups.
- Combine series and parallel resistances iteratively
After calculating all parallel combinations, sum them up for the series connections. Repeat grouping and calculating until you have a single equivalent resistance for terminals F and B.
- Final equivalent resistance calculation
Calculate the final equivalent resistance using the consolidated values from the previous steps.
The equivalent resistance between terminals F and B is $R_{eq} = 1992 , \Omega$.
More Information
The equivalent resistance can vary depending on how resistors are connected. In this case, careful consideration of series and parallel combinations allowed for the calculation of a total resistance.
Tips
- Misidentifying resistors as being in series or parallel.
- Not applying the correct formulas for series and parallel resistances.
- Forgetting to convert the final equivalent resistance back to ohms if the resistor values are normalized.
AI-generated content may contain errors. Please verify critical information