Find the distance between the parallel lines: 3x - 4y + 7 = 0 and 3x - 4y + 5 = 0.
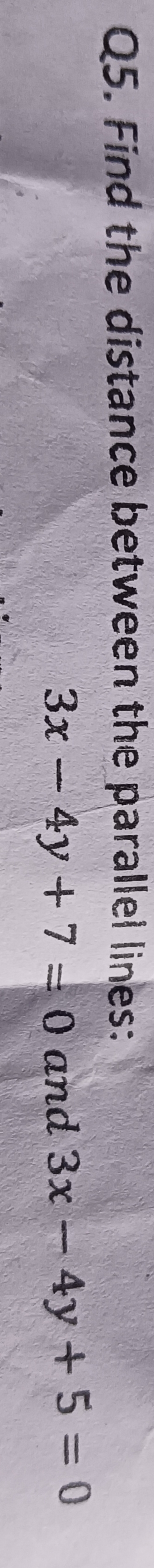
Understand the Problem
The question is asking to find the distance between two parallel lines given by their equations. We will utilize the formula for the distance between two parallel lines in the standard form.
Answer
The distance between the parallel lines is \( \frac{2}{5} \).
Answer for screen readers
The distance between the parallel lines is ( \frac{2}{5} ).
Steps to Solve
- Identify the equations of the lines
The equations of the parallel lines are:
$$ 3x - 4y + 7 = 0 $$
$$ 3x - 4y + 5 = 0 $$
- Use the distance formula for parallel lines
The distance ( d ) between two parallel lines in the form ( Ax + By + C_1 = 0 ) and ( Ax + By + C_2 = 0 ) is given by the formula:
$$ d = \frac{|C_2 - C_1|}{\sqrt{A^2 + B^2}} $$
Here, ( A = 3 ), ( B = -4 ), ( C_1 = 7 ), and ( C_2 = 5 ).
- Calculate the difference in the constant terms
First, compute ( |C_2 - C_1| ):
$$ |5 - 7| = | -2 | = 2 $$
- Calculate ( A^2 + B^2 )
Now compute ( A^2 + B^2 ):
$$ A^2 + B^2 = 3^2 + (-4)^2 = 9 + 16 = 25 $$
- Substitute values into the distance formula
Now substitute the values into the distance formula:
$$ d = \frac{2}{\sqrt{25}} $$
- Simplify the distance
Simplifying gives:
$$ d = \frac{2}{5} $$
The distance between the parallel lines is ( \frac{2}{5} ).
More Information
The distance between two parallel lines is essentially the shortest distance between them, which can be computed using constant values from their equations. The formula used is derived from basic geometric principles involving distance and lines.
Tips
- Confusing the constants ( C_1 ) and ( C_2 ) or mixing up the coefficients of ( x ) and ( y ).
- Forgetting to take the absolute value when calculating ( |C_2 - C_1| ).
AI-generated content may contain errors. Please verify critical information