Find the cube roots of the complex number -8i, giving the answers in the form a + bi, where a and b are real numbers.
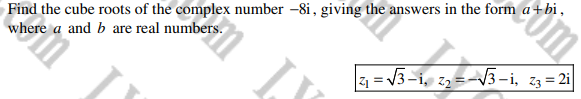
Understand the Problem
The question is asking for the cube roots of the complex number -8i, and specifically wants the answers expressed in the form a + bi, where a and b are real numbers. This involves using the polar form of complex numbers and De Moivre's theorem to find the cube roots.
Answer
The cube roots of $-8i$ are $z_1 = \sqrt{3} - i, z_2 = 2i, z_3 = -\sqrt{3} + i$.
Answer for screen readers
The cube roots of the complex number $-8i$ are:
$$ z_1 = \sqrt{3} - i, \quad z_2 = 2i, \quad z_3 = -\sqrt{3} + i $$
Steps to Solve
- Convert to Polar Form
To find the cube roots of the complex number $-8i$, we first express it in polar form. A complex number $z = re^{i\theta}$, where ( r ) is the modulus and ( \theta ) is the argument.
-
The modulus ( r ) is calculated as: $$ r = \sqrt{(-8)^2 + 0^2} = \sqrt{64} = 8 $$
-
The argument ( \theta ) is found using: $$ \theta = \text{atan2}(y, x) = \text{atan2}(-8, 0) = -\frac{\pi}{2} $$
Thus, we have: $$ z = 8e^{-i\frac{\pi}{2}} $$
- Apply De Moivre's Theorem
To find the cube roots, we use De Moivre's theorem, which states that if ( z = re^{i\theta} ), then the $n$-th roots are given by: $$ z_k = r^{1/n} \cdot e^{i(\theta + 2k\pi)/n} $$
For the cube roots (where ( n = 3 )):
- The modulus for the cube root: $$ r^{1/3} = 8^{1/3} = 2 $$
- Find the Angles for Each Root
We will calculate the argument for each of the three cube roots:
-
For ( k = 0 ): $$ \theta_0 = \frac{-\frac{\pi}{2} + 2(0)\pi}{3} = -\frac{\pi}{6} $$
-
For ( k = 1 ): $$ \theta_1 = \frac{-\frac{\pi}{2} + 2(1)\pi}{3} = \frac{\pi}{2} $$
-
For ( k = 2 ): $$ \theta_2 = \frac{-\frac{\pi}{2} + 2(2)\pi}{3} = \frac{5\pi}{6} $$
- Convert Each Root Back to Rectangular Form
Now we convert each root from polar to rectangular form ( z_k = r\left(\cos(\theta_k) + i\sin(\theta_k)\right) ).
-
For ( k = 0 ): $$ z_0 = 2\left(\cos\left(-\frac{\pi}{6}\right) + i\sin\left(-\frac{\pi}{6}\right)\right) = 2\left(\frac{\sqrt{3}}{2} - i\frac{1}{2}\right) = \sqrt{3} - i $$
-
For ( k = 1 ): $$ z_1 = 2\left(\cos\left(\frac{\pi}{2}\right) + i\sin\left(\frac{\pi}{2}\right)\right) = 2(0 + i) = 2i $$
-
For ( k = 2 ): $$ z_2 = 2\left(\cos\left(\frac{5\pi}{6}\right) + i\sin\left(\frac{5\pi}{6}\right)\right) = 2\left(-\frac{\sqrt{3}}{2} + i\frac{1}{2}\right) = -\sqrt{3} + i $$
- Compile the Results
The cube roots of $-8i$ are: $$ z_1 = \sqrt{3} - i, \quad z_2 = 2i, \quad z_3 = -\sqrt{3} + i $$
The cube roots of the complex number $-8i$ are:
$$ z_1 = \sqrt{3} - i, \quad z_2 = 2i, \quad z_3 = -\sqrt{3} + i $$
More Information
The cube roots of complex numbers are points on the complex plane, evenly spaced on a circle of radius equivalent to the cube root of the original modulus. In this case, the roots are derived from the representation of the original number in polar coordinates, illustrating a connection between multiplication of complex numbers and rotational symmetry.
Tips
- Confusing the angles or forgetting to apply the periodic nature of the argument when calculating multiple roots.
- Neglecting to convert from polar to rectangular form properly.
- Not adjusting for any signs when evaluating sine and cosine at specific angles.
AI-generated content may contain errors. Please verify critical information