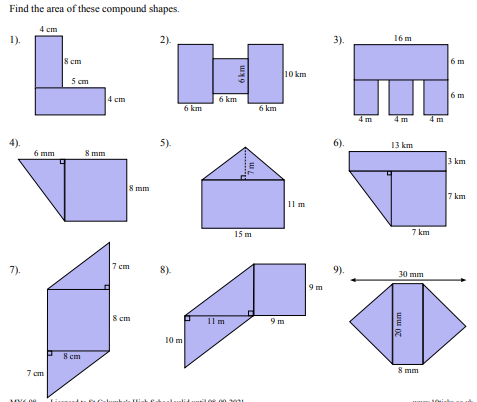
Find the area of these compound shapes.

Understand the Problem

The question asks to calculate the area of several compound shapes, by splitting each shape into basic shapes such as rectangles, squares, triangles, and then summing their areas to obtain the total area of the compound shape.

Answer

1) $36 \text{ cm}^2$ 2) $156 \text{ km}^2$ 3) $168 \text{ m}^2$ 4) $88 \text{ mm}^2$ 5) $217.5 \text{ m}^2$ 6) $63.5 \text{ km}^2$ 7) $120 \text{ cm}^2$ 8) $136 \text{ m}^2$ 9) $380 \text{ mm}^2$

Steps to Solve

Calculate the area of shape 1

Shape 1 can be split into two rectangles. The top rectangle has dimensions $4 \text{ cm} \times 4 \text{ cm}$, and the bottom rectangle has dimensions $5 \text{ cm} \times 4 \text{ cm}$. Area of top rectangle = $4 \times 4 = 16 \text{ cm}^2$ Area of bottom rectangle = $5 \times 4 = 20 \text{ cm}^2$ Total area = $16 + 20 = 36 \text{ cm}^2$

Calculate the area of shape 2

Shape 2 can be split into three rectangles. The two side rectangles have dimensions $6 \text{ km} \times 10 \text{ km}$, and the middle rectangle has dimensions $6 \text{ km} \times 6 \text{ km}$. Area of each side rectangle = $6 \times 10 = 60 \text{ km}^2$ Area of middle rectangle = $6 \times 6 = 36 \text{ km}^2$ Total area = $60 + 60 + 36 = 156 \text{ km}^2$

Calculate the area of shape 3

Shape 3 can be split into one large rectangle and three smaller rectangles. The large rectangle has dimensions $16 \text{ m} \times 6 \text{ m}$, and each of the three smaller rectangles has dimensions $4 \text{ m} \times 6 \text{ m}$. Area of large rectangle = $16 \times 6 = 96 \text{ m}^2$ Area of each small rectangle = $4 \times 6 = 24 \text{ m}^2$ Total area = $96 + 24 + 24 + 24 = 168 \text{ m}^2$

Calculate the area of shape 4

Shape 4 can be split into a triangle and a rectangle. The triangle has a base of $6 \text{ mm}$ and a height of $8 \text{ mm}$, and the rectangle has dimensions $8 \text{ mm} \times 8 \text{ mm}$. Area of triangle = $\frac{1}{2} \times 6 \times 8 = 24 \text{ mm}^2$ Area of rectangle = $8 \times 8 = 64 \text{ mm}^2$ Total area = $24 + 64 = 88 \text{ mm}^2$

Calculate the area of shape 5

Shape 5 can be split into a triangle and a rectangle. The triangle has a base of $15 \text{ m}$ and a height of $7 \text{ m}$, and the rectangle has dimensions $15 \text{ m} \times 11 \text{ m}$. Area of triangle = $\frac{1}{2} \times 15 \times 7 = 52.5 \text{ m}^2$ Area of rectangle = $15 \times 11 = 165 \text{ m}^2$ Total area = $52.5 + 165 = 217.5 \text{ m}^2$

Calculate the area of shape 6

Shape 6 can be split into a triangle and a rectangle. The triangle has a base of $7 \text{ km}$ and a height of $7 \text{ km}$, and the rectangle has dimensions $13 \text{ km} \times 3 \text{ km}$. Area of triangle = $\frac{1}{2} \times 7 \times 7 = 24.5 \text{ km}^2$ Area of rectangle = $13 \times 3 = 39 \text{ km}^2$ Total area = $24.5 + 39 = 63.5 \text{ km}^2$

Calculate the area of shape 7

Shape 7 can be split into a triangle, a rectangle, and another triangle. The two triangles are identical. Each triangle has a base of $7 \text{ cm}$ and a height of $8 \text{ cm}$, and the rectangle has dimensions $8 \text{ cm} \times 8 \text{ cm}$. Area of each triangle = $\frac{1}{2} \times 7 \times 8 = 28 \text{ cm}^2$ Area of rectangle = $8 \times 8 = 64 \text{ cm}^2$ Total area = $28 + 28 + 64 = 120 \text{ cm}^2$

Calculate the area of shape 8

Shape 8 can be split into a triangle and a rectangle. The triangle has a base of $11 \text{ m}$ and a height of $10 \text{ m}$, and the rectangle has dimensions $9 \text{ m} \times 9 \text{ m}$. Area of triangle = $\frac{1}{2} \times 11 \times 10 = 55 \text{ m}^2$ Area of rectangle = $9 \times 9 = 81 \text{ m}^2$ Total area = $55 + 81 = 136 \text{ m}^2$

Calculate the area of shape 9

Shape 9 can be split into a rectangle and two triangles. The two triangles are identical. The rectangle has dimensions $8 \text{ mm} \times 20 \text{ mm}$. The two triangles combined can be viewed as one diamond shape with diagonals of length $20 \text{ mm}$ and $(30-8) = 22 \text{ mm}$. The area of the two triangles is $\frac{1}{2} \times 20 \times 22 = 220 \text{ mm}^2$ Area of rectangle = $8 \times 20 = 160 \text{ mm}^2$ Total area = $220 + 160 = 380 \text{ mm}^2$

$36 \text{ cm}^2$
$156 \text{ km}^2$
$168 \text{ m}^2$
$88 \text{ mm}^2$
$217.5 \text{ m}^2$
$63.5 \text{ km}^2$
$120 \text{ cm}^2$
$136 \text{ m}^2$
$380 \text{ mm}^2$

More Information

The key to solving these kinds of problems is correctly decomposing compound shapes into simpler shapes for which area formulas are known. Accuracy in reading the dimensions from the diagram is also crucial for obtaining the correct numerical answer.

Tips

A common mistake is misinterpreting the dimensions or incorrectly splitting the compound shape. It's important to double-check the measurements and ensure the split shapes cover the entire area without overlaps. Another common mistake is using the wrong formula for area, especially for triangles (forgetting the 1/2 factor). Also, forgetting the units.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!