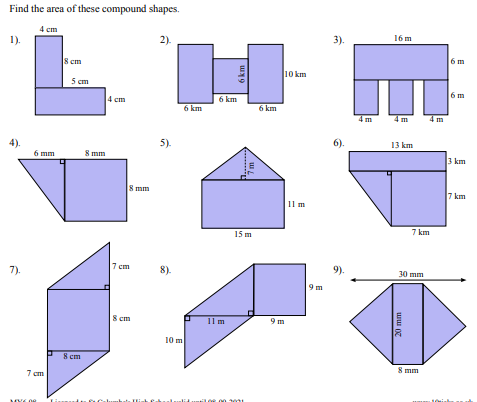
Find the area of these compound shapes.

Understand the Problem

The question asks you to calculate the area of several compound shapes. Each shape is made up of rectangles, triangles, and squares! You must find the area of the individual shapes and either add them or subtract them to find the areas of the shapes.

Answer

1) $56 \text{ cm}^2$ 2) $132 \text{ km}^2$ 3) $24 \text{ m}^2$ 4) $88 \text{ mm}^2$ 5) $217.5 \text{ m}^2$ 6) $63.5 \text{ km}^2$ 7) $120 \text{ cm}^2$ 8) $154 \text{ m}^2$ 9) $380 \text{ mm}^2$

Steps to Solve

Calculate the area of shape 1

The shape is made up of two rectangles. We will call the top rectangle A and the botoom rectangle B. Area of rectangle A = length * width = $4 \text{ cm} * 4 \text{ cm} = 16 \text{ cm}^2$ Area of rectangle B = length * width = $8 \text{ cm} * 5 \text{ cm} = 40 \text{ cm}^2$ Total Area = Area A + Area B = $16 \text{ cm}^2 + 40 \text{ cm}^2 = 56 \text{ cm}^2$

Calculate the area of shape 2

The shape is made up of three rectangles. We will call the left rectangle A, middle rectangle B, and right rectangle C. Area of rectangle A = length * width = $6 \text{ km} * 6 \text{ km} = 36 \text{ km}^2$ Area of rectangle B = length * width = $6 \text{ km} * 6 \text{ km} = 36 \text{ km}^2$ Area of rectangle C = length * width = $6 \text{ km} * 10 \text{ km} = 60 \text{ km}^2$ Total Area = Area A + Area B + Area C = $36 \text{ km}^2 + 36 \text{ km}^2 + 60 \text{ km}^2 = 132 \text{ km}^2$

Calculate the area of shape 3

The shape is made up of a large rectangle minus three smaller rectangles. We will call the large rectangle A and the smaller rectangles B, C, and D. Area of rectangle A = length * width = $16 \text{ m} * 6 \text{ m} = 96 \text{ m}^2$ Area of rectangles B, C, and D = length * width = $4 \text{ m} * 6 \text{ m} = 24 \text{ m}^2$ Total Area = Area A - Area B - Area C - Area D = $96 \text{ m}^2 - 24 \text{ m}^2 - 24 \text{ m}^2 - 24 \text{ m}^2 = 24 \text{ m}^2$

Alternatively: there are 2 skinny retangles. The total width of these rectangles is $16 - 4 - 4 - 4 = 4$. So the area of these two retangles is $4 \text{ m} * 6 \text{ m} = 24 \text{ m}^2$. The final answer is $24 \text{ m}^2 + 0 = 24 \text{ m}^2$.

Calculate the area of shape 4

The shape is made up of a triangle and a rectangle. We will call the triangle A and the rectangle B. Area of Triangle A = $0.5 * \text{base} * \text{height} = 0.5 * 6 \text{ mm} * 8 \text{ mm} = 24 \text{ mm}^2$ Area of Rectangle B = length * width = $8 \text{ mm} * 8 \text{ mm} = 64 \text{ mm}^2$ Total Area = Area A + Area B = $24 \text{ mm}^2 + 64 \text{ mm}^2 = 88 \text{ mm}^2$

Calculate the area of shape 5

The shape is made up of a triangle and a rectangle. We will call the triangle A and the rectangle B. Area of Triangle A = $0.5 * \text{base} * \text{height} = 0.5 * 15 \text{ m} * 7 \text{ m} = 52.5 \text{ m}^2$ Area of Rectangle B = length * width = $15 \text{ m} * 11 \text{ m} = 165 \text{ m}^2$ Total Area = Area A + Area B = $52.5 \text{ m}^2 + 165 \text{ m}^2 = 217.5 \text{ m}^2$

Calculate the area of shape 6

The shape is made up of a triangle and a rectangle. We will call the triangle A and the rectangle B. Area of Triangle A = $0.5 * \text{base} * \text{height} = 0.5 * 7 \text{ km} * 7 \text{ km} = 24.5 \text{ km}^2$ Area of Rectangle B = length * width = $13 \text{ km} * 3 \text{ km} = 39 \text{ km}^2$ Total Area = Area A + Area B = $24.5 \text{ km}^2 + 39 \text{ km}^2 = 63.5 \text{ km}^2$

Calculate the area of shape 7

The shape is made up of a parallelogram and a square. We will call the parallelogram A and the square B. Area of Parallelogram A = base * height = $7 \text{ cm} * 8 \text{ cm} = 56 \text{ cm}^2$ Area of Square B = length * width = $8 \text{ cm} * 8 \text{ cm} = 64 \text{ cm}^2$ Total Area = Area A + Area B = $56 \text{ cm}^2 + 64 \text{ cm}^2 = 120 \text{ cm}^2$

Calculate the area of shape 8

The shape is made up of a triangle and a rectangle. We will call the triangle A and the rectangle B. Area of Triangle A = $0.5 * \text{base} * \text{height} = 0.5 * 11 \text{ m} * 10 \text{ m} = 55 \text{ m}^2$ Area of Rectangle B = length * width = $9 \text{ m} * 11 \text{ m} = 99 \text{ m}^2$ Total Area = Area A + Area B = $55 \text{ m}^2 + 99 \text{ m}^2 = 154 \text{ m}^2$

Calculate the area of shape 9

The shape is made up of a rectangle and two triangles. We will call the rectangle A and the triangles B and C. Note that triangles B and C are congruent, so they have the same area! Area of Rectangle A = length * width = $8 \text{ mm} * 20 \text{ mm} = 160 \text{ mm}^2$ The total base for the combined triangle is $30 \text{ mm} - 8 \text{ mm} = 22 \text{ mm}$. So the base for each individual triangle is $22 \text{ mm} / 2 = 11 \text{ mm}$. Area of Triangle B = $0.5 * \text{base} * \text{height} = 0.5 * 11 \text{ mm} * 20 \text{ mm} = 110 \text{ mm}^2$. Since Area of Triangle B = Area of triangle C, Area C = $110 \text{ mm}^2$ Total Area = Area A + Area B + Area C = $160 \text{ mm}^2 + 110 \text{ mm}^2 + 110 \text{ mm}^2 = 380 \text{ mm}^2$

$56 \text{ cm}^2$
$132 \text{ km}^2$
$24 \text{ m}^2$
$88 \text{ mm}^2$
$217.5 \text{ m}^2$
$63.5 \text{ km}^2$
$120 \text{ cm}^2$
$154 \text{ m}^2$
$380 \text{ mm}^2$

More Information

The area of compound shapes can be found by dividing the shapes into smaller, more manageable shapes such as rectangles, squares, triangles and parallelograms. Then finding the area of the individual shapes and summing them all together. Note that for some of the problems, we will have to subtract a shape to find the final area.

Tips

One common mistake is to confuse perimeter and area. Perimeter is the distance around a shape, while area is the measure of the surface of a shape. Another common mistake is using the wrong units. Make sure to include units in your calculation and answer!.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!