Find the area of the region bounded by the curves f(x) = sin(x), g(x) = cos(x), x = 0, and x = π/2.
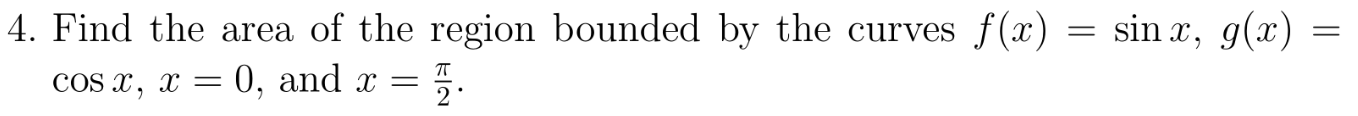
Understand the Problem
The question is asking to find the area of a region bounded by the curves given by the sine and cosine functions, along with two vertical lines at x = 0 and x = π/2. This involves calculating the definite integral of the difference between the two curves over the specified interval.
Answer
The area is given by the expression \( A = 2 - 2\sqrt{2} \).
Answer for screen readers
The area of the region bounded by the curves is: $$ A = 2 - 2\sqrt{2} $$
Steps to Solve
- Identify the curves and boundaries
The curves are ( f(x) = \sin x ) and ( g(x) = \cos x ). The vertical lines are at ( x = 0 ) and ( x = \frac{\pi}{2} ).
- Determine the area to be calculated
The area between the curves from ( x = 0 ) to ( x = \frac{\pi}{2} ) is given by the integral: $$ A = \int_{0}^{\frac{\pi}{2}} (f(x) - g(x)) , dx $$
- Find the points of intersection
Set ( \sin x = \cos x ) to find the intersection points within the interval. This occurs at: $$ x = \frac{\pi}{4} $$
- Set up the integral
Since ( \sin x ) is above ( \cos x ) in the interval ( \left[0, \frac{\pi}{4}\right] ) and below in ( \left[\frac{\pi}{4}, \frac{\pi}{2}\right] ), we calculate the area as: $$ A = \int_{0}^{\frac{\pi}{4}} (\sin x - \cos x) , dx + \int_{\frac{\pi}{4}}^{\frac{\pi}{2}} (\cos x - \sin x) , dx $$
- Calculate the first integral
Calculate the integral from ( 0 ) to ( \frac{\pi}{4} ): $$ \int (\sin x - \cos x) , dx = -\cos x - \sin x $$
Evaluate it from ( 0 ) to ( \frac{\pi}{4} ): $$ \left[-\cos\left(\frac{\pi}{4}\right) - \sin\left(\frac{\pi}{4}\right)\right] - \left[-\cos(0) - \sin(0)\right] $$
This simplifies to: $$ \left[-\frac{\sqrt{2}}{2} - \frac{\sqrt{2}}{2}\right] - [-1 - 0] = -\sqrt{2} + 1 $$
- Calculate the second integral
Calculate the integral from ( \frac{\pi}{4} ) to ( \frac{\pi}{2} ): $$ \int (\cos x - \sin x) , dx = \sin x + \cos x $$
Evaluate it from ( \frac{\pi}{4} ) to ( \frac{\pi}{2} ): $$ \left[\sin\left(\frac{\pi}{2}\right) + \cos\left(\frac{\pi}{2}\right)\right] - \left[\sin\left(\frac{\pi}{4}\right) + \cos\left(\frac{\pi}{4}\right)\right] $$
This simplifies to: $$ [1 + 0] - \left[\frac{\sqrt{2}}{2} + \frac{\sqrt{2}}{2}\right] = 1 - \sqrt{2} $$
- Combine the results
Add both areas: $$ A = (-\sqrt{2} + 1) + (1 - \sqrt{2}) = 2 - 2\sqrt{2} $$
The area of the region bounded by the curves is: $$ A = 2 - 2\sqrt{2} $$
More Information
The area represents the region between the sine and cosine functions over the specified interval. The sine curve starts below the cosine curve at ( x = 0 ) and then crosses it at ( x = \frac{\pi}{4} ), leading to this area calculation.
Tips
- Forgetting to evaluate the integrals correctly from the specified limits.
- Not taking into account where one function is above the other within the specified interval.
- Miscalculating trigonometric values at key points, such as ( \sin\left(\frac{\pi}{4}\right) ) or ( \cos\left(\frac{\pi}{4}\right) ).
AI-generated content may contain errors. Please verify critical information