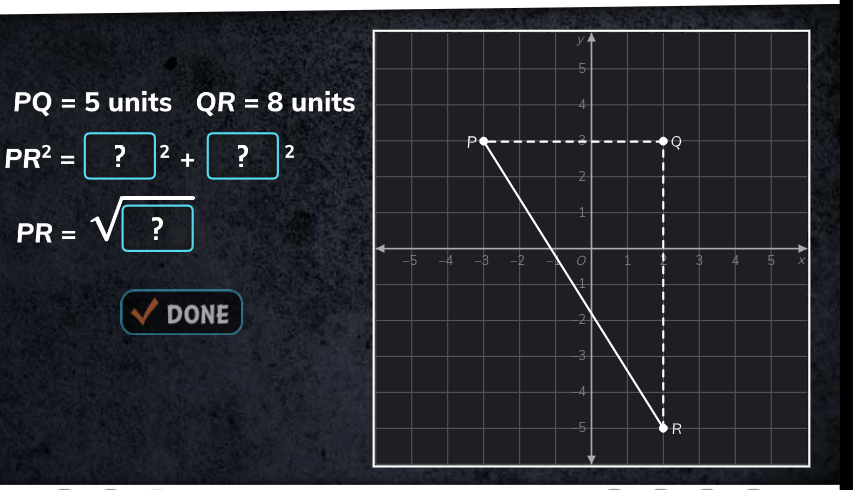
Find PR using the Pythagorean theorem. Given PQ = 5 units and QR = 8 units, calculate PR.
Understand the Problem
The question involves finding the distance PR using the Pythagorean theorem. We know the lengths PQ and QR, and we need to derive PR by determining the missing lengths in the right triangle formed by points P, Q, and R.
Answer
$PR = \sqrt{89}$
Answer for screen readers
The length of $PR$ is $\sqrt{89}$ units.
Steps to Solve
- Identify the lengths given
From the problem, we have:
- Length of $PQ = 5$ units
- Length of $QR = 8$ units
- Apply the Pythagorean theorem
In a right triangle, the Pythagorean theorem states:
$$ PR^2 = PQ^2 + QR^2 $$
Substituting the known lengths:
$$ PR^2 = 5^2 + 8^2 $$
- Calculate the squares of the lengths
Calculating the squares:
$$ 5^2 = 25 $$
$$ 8^2 = 64 $$
- Add the squares together
Now, add the results:
$$ PR^2 = 25 + 64 $$
This yields:
$$ PR^2 = 89 $$
- Find the square root to get PR
To find the length $PR$, we take the square root:
$$ PR = \sqrt{89} $$
The length of $PR$ is $\sqrt{89}$ units.
More Information
The Pythagorean theorem is a fundamental principle in geometry that allows us to calculate the lengths of sides in a right triangle. In this case, we found that the length from point P to R is approximately 9.43 units, since $\sqrt{89} \approx 9.43$.
Tips
- Forget to square the values: Always remember to square the lengths before adding them.
- Incorrect application of the theorem: Ensure you apply the Pythagorean theorem correctly by using the right triangle's side lengths.
AI-generated content may contain errors. Please verify critical information