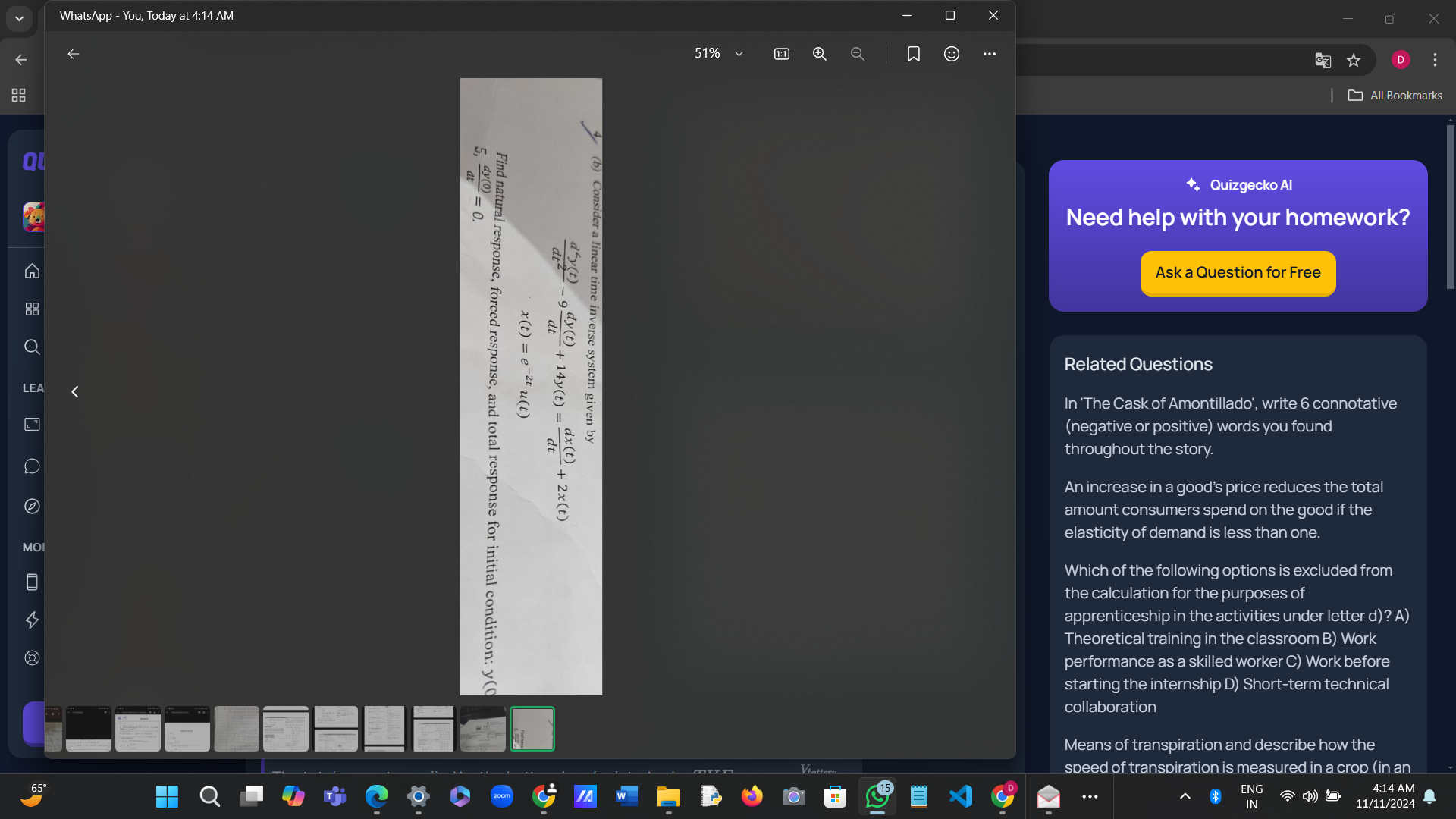
Find natural responses, forced responses, and total responses for the system given by the differential equation dx(t)/dt + 4x(t) = u(t) with x(0) = -2z u(0) and x(0) = 0.

Steps to Solve

1. Identify the System Type This is a first-order linear time-invariant (LTI) system described by the differential equation: $$ \frac{dx(t)}{dt} + 4x(t) = u(t) $$

2. Formulate the Homogeneous Equation The homogeneous equation (natural response) is obtained by setting the input ( u(t) = 0 ): $$ \frac{dx_h(t)}{dt} + 4x_h(t) = 0 $$

3. Solve the Homogeneous Equation To solve for the natural response, separate variables and integrate: $$ \frac{dx_h(t)}{x_h(t)} = -4 dt $$ Integrating both sides gives: $$ \ln|x_h(t)| = -4t + C $$ This simplifies to: $$ x_h(t) = Ce^{-4t} $$

4. Determine the Forced Response For the forced response, we need to solve the complete equation. The steady-state solution can be guessed as ( x_f(t) = K ): Substituting into the differential equation gives: $$ 0 + 4K = u(t) $$ If ( u(t) = 1 ) (step function), then: $$ K = \frac{1}{4} $$

5. Combine Responses The total response ( x(t) ) is the sum of the natural and forced responses, considering the initial conditions: $$ x(t) = x_h(t) + x_f(t) = Ce^{-4t} + \frac{1}{4} $$

6. Applying Initial Conditions Using the initial condition ( x(0) = -2z u(0) ): Assuming ( u(0) = 1 ): $$ x(0) = C + \frac{1}{4} = -2z $$ This leads to: $$ C = -2z - \frac{1}{4} $$

7. Final Total Response Now substitute ( C ) back into the total response: $$ x(t) = \left(-2z - \frac{1}{4}\right)e^{-4t} + \frac{1}{4} $$