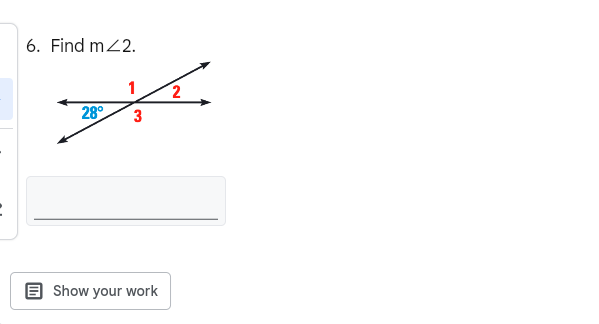
Find m∠2.
Understand the Problem
The question is asking to determine the measure of angle 2 given that angle 1 measures 28 degrees and is situated as an alternate angle with angle 2 across a transversal.
Answer
The measure of angle 2 is $28^\circ$.
Answer for screen readers
The measure of angle 2 is $28^\circ$.
Steps to Solve
-
Identify the Relationship Between Angles Since angle 1 (28 degrees) and angle 2 are alternate interior angles formed by the transversal, they are congruent.
-
Set Up the Equation Because alternate interior angles are congruent, we can write the equation: $$ m \angle 2 = m \angle 1 $$
-
Substitute the Known Value Now substitute the measure of angle 1 into the equation: $$ m \angle 2 = 28^\circ $$
-
State the Measure of Angle 2 Thus, angle 2 measures 28 degrees.
The measure of angle 2 is $28^\circ$.
More Information
Alternate interior angles are always equal when two parallel lines are cut by a transversal. This property helps in solving many geometry problems related to angles.
Tips
- Confusing alternate interior angles with corresponding angles.
- Forgetting that alternate interior angles are equal only when the lines are parallel.
AI-generated content may contain errors. Please verify critical information