Find dy/dx if y² = x² + sin(xy)
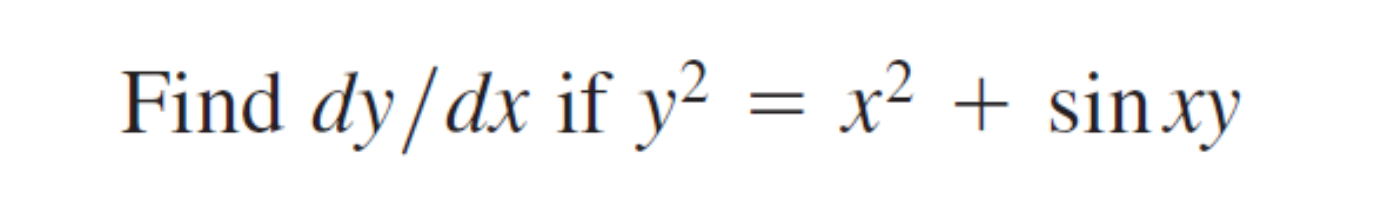
Understand the Problem
The question is asking us to find the derivative of y with respect to x (dy/dx) given the equation y² = x² + sin(xy). This will require implicit differentiation.
Answer
$$ \frac{dy}{dx} = \frac{2x + \cos(xy)y}{2y - \cos(xy)x} $$
Answer for screen readers
The derivative ( \frac{dy}{dx} ) is given by:
$$ \frac{dy}{dx} = \frac{2x + \cos(xy)y}{2y - \cos(xy)x} $$
Steps to Solve
- Differentiate both sides with respect to ( x )
We start by differentiating both sides of the equation ( y^2 = x^2 + \sin(xy) ).
Using implicit differentiation:
$$ \frac{d}{dx}(y^2) = \frac{d}{dx}(x^2 + \sin(xy)) $$
- Apply the chain rule
For the left side, use the chain rule:
$$ 2y \frac{dy}{dx} $$
For the right side, differentiate each term:
- The derivative of ( x^2 ) is ( 2x ).
- For ( \sin(xy) ), we use the product rule:
$$ \frac{d}{dx}(\sin(xy)) = \cos(xy) \left( y + x\frac{dy}{dx} \right) $$
Combining these gives:
$$ 2y \frac{dy}{dx} = 2x + \cos(xy) \left( y + x \frac{dy}{dx} \right) $$
- Rearrange to solve for ( \frac{dy}{dx} )
Get all ( \frac{dy}{dx} ) terms on one side:
$$ 2y \frac{dy}{dx} - \cos(xy) x \frac{dy}{dx} = 2x + \cos(xy) y $$
Factor out ( \frac{dy}{dx} ):
$$ \left( 2y - \cos(xy)x \right) \frac{dy}{dx} = 2x + \cos(xy)y $$
- Isolate ( \frac{dy}{dx} )
Now divide both sides by ( 2y - \cos(xy)x ):
$$ \frac{dy}{dx} = \frac{2x + \cos(xy)y}{2y - \cos(xy)x} $$
The derivative ( \frac{dy}{dx} ) is given by:
$$ \frac{dy}{dx} = \frac{2x + \cos(xy)y}{2y - \cos(xy)x} $$
More Information
This result shows how the rate of change of ( y ) with respect to ( x ) depends not only on ( x ) and ( y ) but also on their interaction through the sine function. Implicit differentiation is a powerful tool when dealing with relations between variables that cannot be explicitly solved for one variable.
Tips
- Forgetting to apply the product rule when differentiating ( \sin(xy) ).
- Not using the chain rule correctly for ( y^2 ).
- Failing to rearrange the equation properly to isolate ( \frac{dy}{dx} ).
