Find all real and imaginary solutions to the equation x^3 - 6x^2 - 13x + 78 = 0.
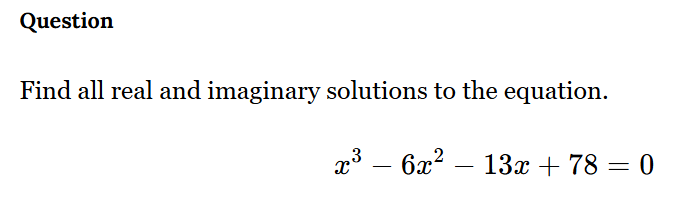
Understand the Problem
The question is asking to find all real and imaginary solutions for the given cubic equation. This involves identifying the roots of the polynomial equation.
Answer
The solutions to the equation are: $$ x = 6, \; x = \sqrt{13}, \; x = -\sqrt{13} $$
Answer for screen readers
The solutions to the equation are: $$ x = 6, \quad x = \sqrt{13}, \quad x = -\sqrt{13} $$
Steps to Solve
-
Identify the polynomial The given equation is a cubic polynomial: $$ x^3 - 6x^2 - 13x + 78 = 0. $$
-
Use the Rational Root Theorem To find possible rational roots, consider the factors of 78. The possible values are ±1, ±2, ±3, ±6, ±13, ±26, ±39, ±78.
-
Test possible roots Substitute the possible rational roots into the polynomial to identify any that yield zero:
- Testing ( x = 6 ): $$ 6^3 - 6(6)^2 - 13(6) + 78 = 216 - 216 - 78 + 78 = 0 $$ Therefore, ( x = 6 ) is a root.
-
Perform synthetic division Now divide the polynomial by ( (x - 6) ):
- The coefficients are ( 1, -6, -13, 78 ).
- Performing synthetic division gives us: $$ x^3 - 6x^2 - 13x + 78 = (x - 6)(x^2 + 0x - 13) $$
-
Solve the quadratic equation To find the other roots, solve: $$ x^2 - 13 = 0 $$ This can be rearranged as: $$ x^2 = 13 $$
-
Find the square roots Taking the square root of both sides yields: $$ x = \sqrt{13} \quad \text{and} \quad x = -\sqrt{13} $$
-
List all solutions The solutions to the equation are: $$ x = 6, \quad x = \sqrt{13}, \quad x = -\sqrt{13} $$
The solutions to the equation are: $$ x = 6, \quad x = \sqrt{13}, \quad x = -\sqrt{13} $$
More Information
This cubic equation has one real root and two real irrational roots. The real roots correspond to points where the graph of the polynomial intersects the x-axis. The Rational Root Theorem helped us identify integer solutions, and synthetic division simplified our polynomial.
Tips
- Forgetting to check all possible rational roots.
- Miscalculating during synthetic division.
- Not verifying the results by substituting them back into the original equation.
AI-generated content may contain errors. Please verify critical information