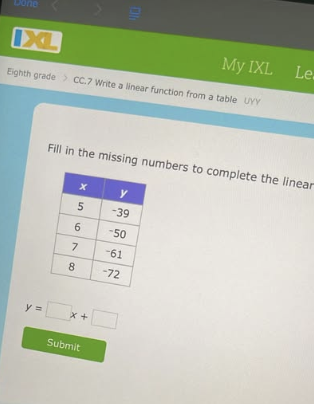
Fill in the missing numbers to complete the linear equation: y = mx + b, given the following values: (5, -39), (6, -50), (7, -61), (8, -72).
Understand the Problem
The question asks us to find the equation of the linear function represented by the table, in the form y = mx + b. We need to determine the values of m (the slope) and b (the y-intercept) based on the given data points and then fill in the blanks. The given points include (5, -39), (6, -50), (7, -61), (8, -72).
Answer
$y = -11x + 16$
Answer for screen readers
$y = -11x + 16$
Steps to Solve
-
Calculate the slope $m$ We can find the slope $m$ using any two points from the table. Let's use the points $(5, -39)$ and $(6, -50)$. The slope formula is: $m = \frac{y_2 - y_1}{x_2 - x_1}$ Plugging in the values: $m = \frac{-50 - (-39)}{6 - 5} = \frac{-50 + 39}{1} = \frac{-11}{1} = -11$ So, the slope $m$ is $-11$.
-
Find the y-intercept $b$ Now that we have the slope, we can use the point-slope form of a linear equation, $y = mx + b$, and one of the points from the table to solve for $b$. Let's use the point $(5, -39)$ and the slope $m = -11$. $-39 = (-11)(5) + b$ $-39 = -55 + b$ $b = -39 + 55$ $b = 16$ So, the y-intercept $b$ is $16$.
-
Write the equation Now we have both the slope $m = -11$ and the y-intercept $b = 16$. We can plug these values into the equation $y = mx + b$ to get the linear equation: $y = -11x + 16$
$y = -11x + 16$
More Information
The equation represents a line with a negative slope, which means that as $x$ increases, $y$ decreases, as shown in the table. The y-intercept is the point where the line crosses the y-axis, which is at $y = 16$.
Tips
A common mistake is to incorrectly calculate the slope by swapping the $x$ and $y$ values in the slope formula, or by miscalculating the change in $x$ or $y$. Also, when solving for the y-intercept, it's important to substitute the values correctly and solve the equation carefully.
AI-generated content may contain errors. Please verify critical information