Factorise completely $x^3+6x^2y+3xy^2-10y^3$
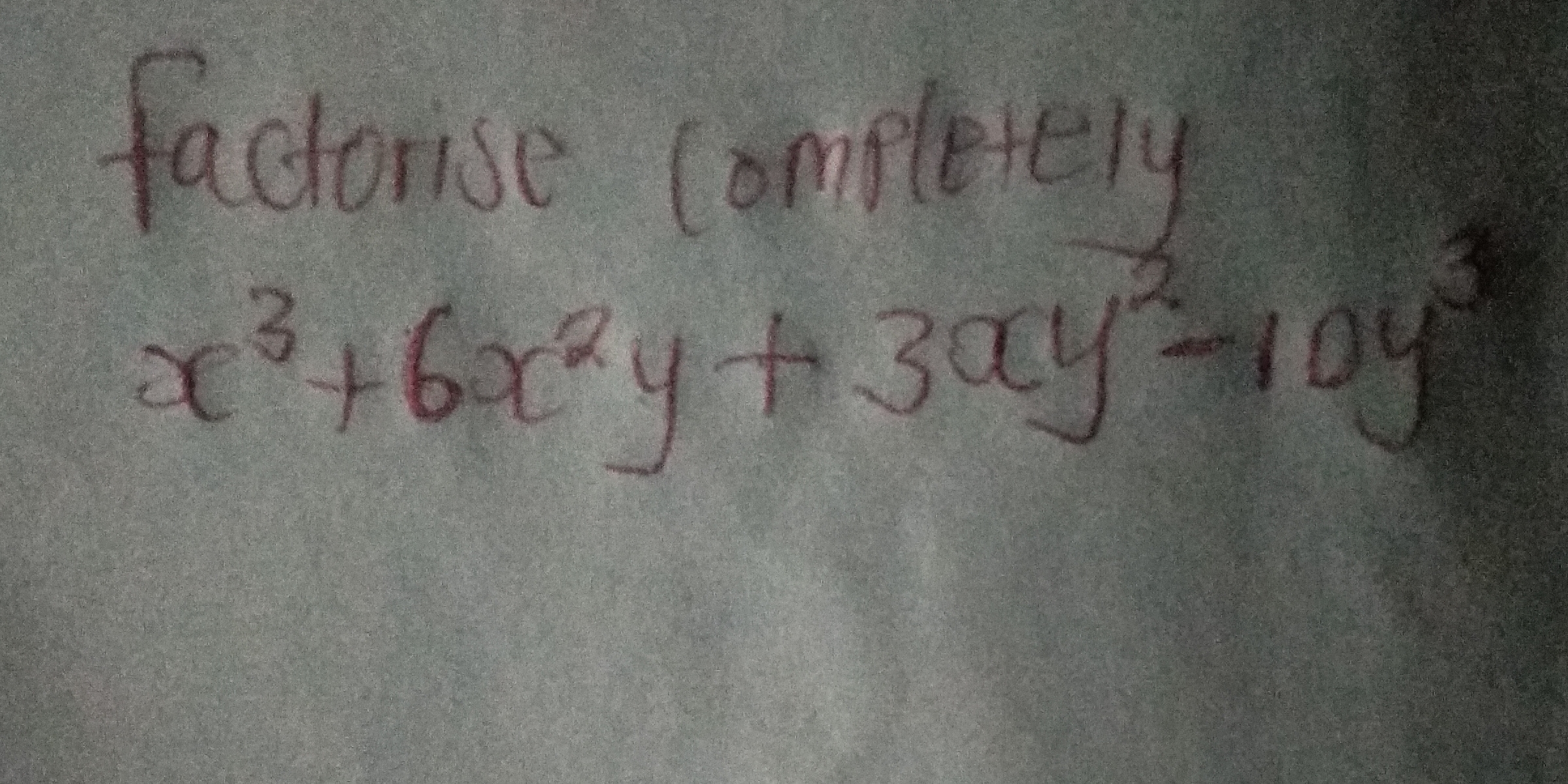
Understand the Problem
The question asks to factorize the given expression completely. This means we need to find expressions that, when multiplied together, give the original expression.
Answer
$(x - y)(x + 2y)(x + 5y)$
Answer for screen readers
$(x - y)(x + 2y)(x + 5y)$
Steps to Solve
- Look for a simple root
We can try to find a value for $\frac{x}{y}$ that makes the polynomial equal to zero. By trying simple integer values, we find that if $x = y$, then the polynomial becomes $1 + 6 + 3 - 10 = 0$. Therefore, $x-y$ is a factor. However, the equation is homogenous of degree 3, so let's try $x = ay$.
- Substitute $x = ay$ into the expression
Substituting $x = ay$ into the expression $x^3 + 6x^2y + 3xy^2 - 10y^3$, we get:
$ (ay)^3 + 6(ay)^2y + 3(ay)y^2 - 10y^3 = a^3y^3 + 6a^2y^3 + 3ay^3 - 10y^3 $
- Factor out $y^3$
$ y^3 (a^3 + 6a^2 + 3a - 10) $
- Find a root of the cubic
Now we need to find a root of the cubic $a^3 + 6a^2 + 3a - 10$. By trying integer values, we find that $a=1$ is a root because $1 + 6 + 3 - 10 = 0$. This means that $(a-1)$ is a factor. So, $x=y$ is a root.
- Perform polynomial division
Now, perform polynomial division to divide $a^3 + 6a^2 + 3a - 10$ by $(a-1)$:
$ \frac{a^3 + 6a^2 + 3a - 10}{a - 1} = a^2 + 7a + 10 $
- Factor the quadratic
Factor the quadratic $a^2 + 7a + 10$:
$ a^2 + 7a + 10 = (a + 2)(a + 5) $
- Rewrite the expression
Now we can rewrite the original expression as:
$ x^3 + 6x^2y + 3xy^2 - 10y^3 = y^3(a - 1)(a + 2)(a + 5) $
Since $a = \frac{x}{y}$:
$ y^3 (\frac{x}{y} - 1)(\frac{x}{y} + 2)(\frac{x}{y} + 5) = (x - y)(x + 2y)(x + 5y) $
$(x - y)(x + 2y)(x + 5y)$
More Information
The given cubic expression in two variables is a homogeneous polynomial of degree 3. Factoring it involves finding three linear factors.
Tips
A common mistake is to stop after finding the first factor, either $(x-y)$ or $(x+2y)$ or $(x+5y)$. Complete factorization requires finding all three linear factors. Another common mistake involves performing incorrect polynomial long division.
AI-generated content may contain errors. Please verify critical information