Factor the polynomial $104y^4 - 140y^3 + 400$
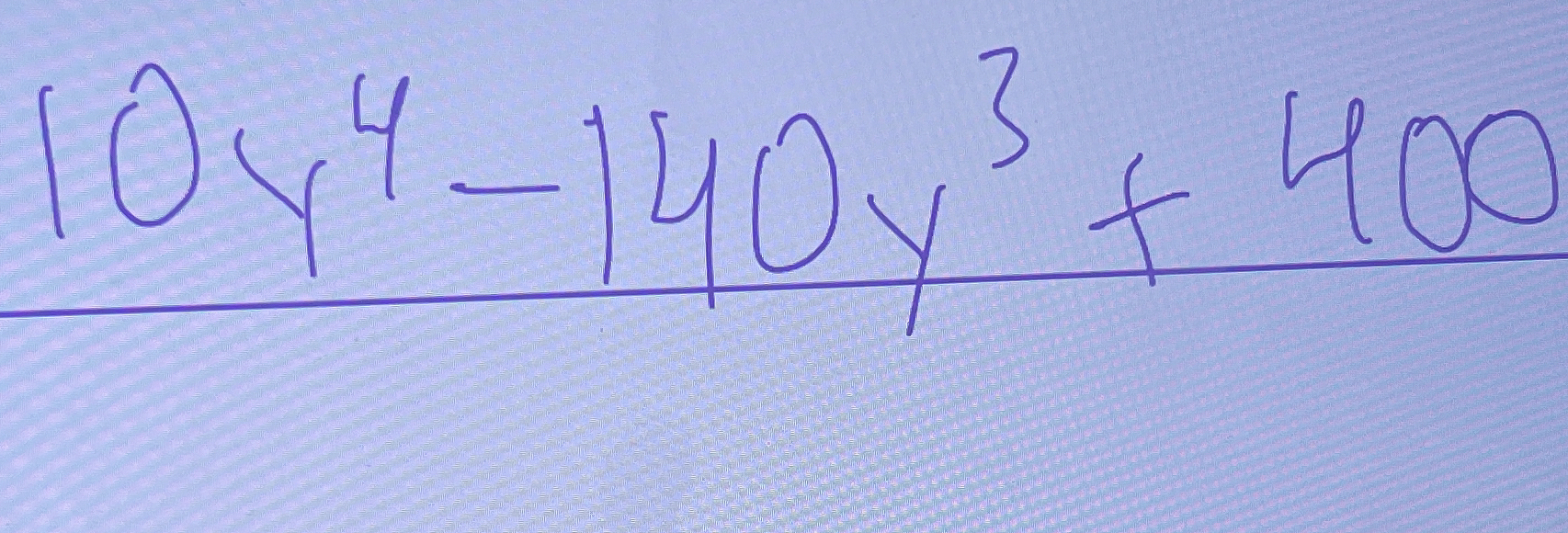
Understand the Problem
The question asks to factor the polynomial $104y^4 - 140y^3 + 400$. We need to find the common factors and simplify the expression.
Answer
$4(26y^4 - 35y^3 + 100)$
Answer for screen readers
$4(26y^4 - 35y^3 + 100)$
Steps to Solve
- Find the greatest common factor (GCF) of the coefficients
The coefficients are 104, -140, and 400.
The prime factorization of 104 is $2^3 \cdot 13$.
The prime factorization of 140 is $2^2 \cdot 5 \cdot 7$.
The prime factorization of 400 is $2^4 \cdot 5^2$.
The greatest common factor is $2^2 = 4$.
- Factor out the GCF from the polynomial
Factor out 4 from each term:
$104y^4 - 140y^3 + 400 = 4(26y^4 - 35y^3 + 100)$
- Check if the remaining polynomial can be factored further
The polynomial $26y^4 - 35y^3 + 100$ does not appear to be easily factorable using simple techniques such as factoring by grouping or recognizing special forms. Since the instructions only asked to factor the expression, we can assume this is the final answer.
$4(26y^4 - 35y^3 + 100)$
More Information
Factoring is the process of breaking down a polynomial into simpler expressions (factors) such that when these factors are multiplied together, they result in the original polynomial. This is the reverse process of expanding or distributing.
Tips
A common mistake is not factoring out the greatest common factor completely. In this case, failing to recognize that all coefficients are divisible by 4 would be an error. Also, some might try to further factor the polynomial inside the parenthesis, which is not easily factorable using simple methods.
AI-generated content may contain errors. Please verify critical information