Factor the expression completely: -p² + 9p - 20.
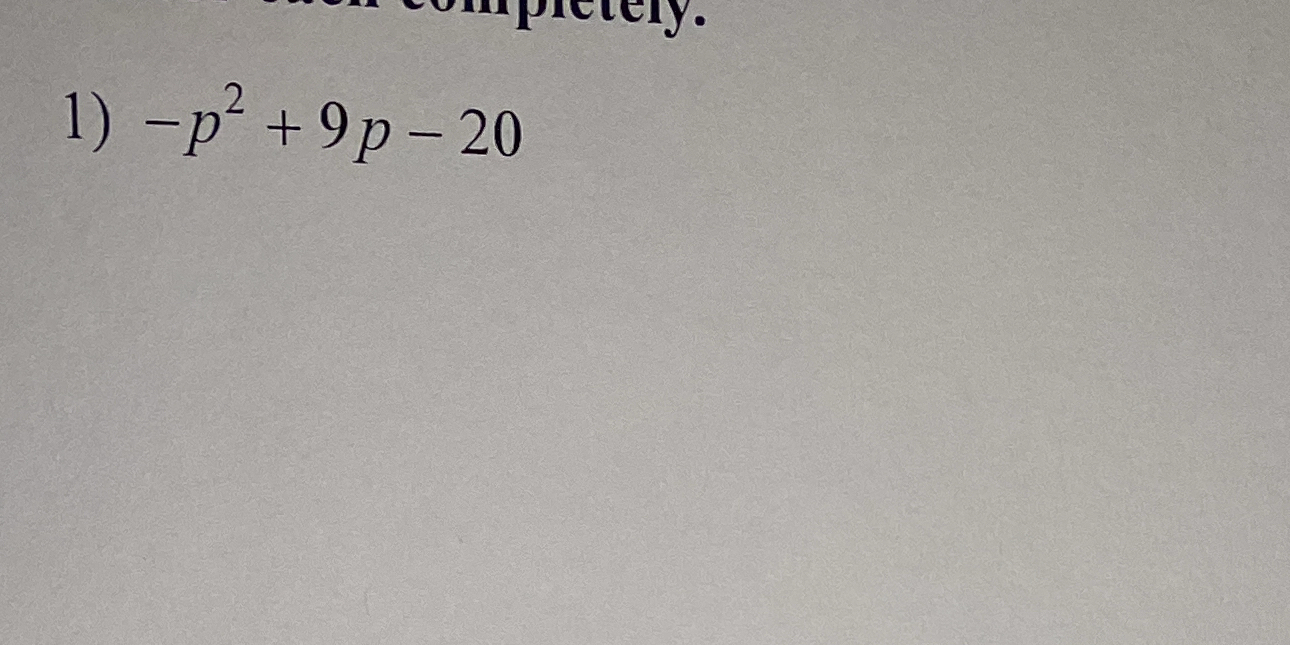
Understand the Problem
The question asks for the complete factorization of the quadratic expression -p² + 9p - 20.
Answer
The complete factorization is: $$ -(p - 4)(p - 5) $$
Answer for screen readers
The complete factorization of the expression is:
$$ -(p - 4)(p - 5) $$
Steps to Solve
- Rearranging the Expression
First, we can factor out a negative sign from the entire expression to make it easier to factor:
$$ -p^2 + 9p - 20 = -1(p^2 - 9p + 20) $$
- Factoring the Quadratic
Next, we need to factor the quadratic $p^2 - 9p + 20$. We need two numbers that multiply to 20 and add up to -9.
The numbers that work are -4 and -5. Thus, we can write:
$$ p^2 - 9p + 20 = (p - 4)(p - 5) $$
- Combining the Factors
Now, we can combine this back with the negative sign we factored out previously:
$$ -1(p^2 - 9p + 20) = -1((p - 4)(p - 5)) $$
So, the complete factorization of the expression is:
$$ -(p - 4)(p - 5) $$
The complete factorization of the expression is:
$$ -(p - 4)(p - 5) $$
More Information
Factoring is a fundamental skill in algebra that helps simplify expressions and solve equations. Understanding how to manipulate and factor quadratics is crucial for higher mathematics.
Tips
- Forgetting to factor out the negative sign, which can lead to missing solutions when solving equations.
- Confusing the signs of factors when finding pairs that multiply to a positive constant but add to a negative linear coefficient.
AI-generated content may contain errors. Please verify critical information