Factor d³ + s³ completely.
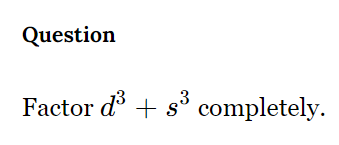
Understand the Problem
The question is asking to factor the algebraic expression d³ + s³ completely. This involves applying the formula for the sum of cubes.
Answer
The completely factored form of \( d^3 + s^3 \) is \( (d + s)(d^2 - ds + s^2) \).
Answer for screen readers
The completely factored form of ( d^3 + s^3 ) is:
$$ (d + s)(d^2 - ds + s^2) $$
Steps to Solve
-
Identify the sum of cubes formula
The formula for factoring a sum of cubes is:
$$ a^3 + b^3 = (a + b)(a^2 - ab + b^2) $$
In this case, let ( a = d ) and ( b = s ). -
Apply the formula
Substituting ( a ) and ( b ) into the formula, we get:
$$ d^3 + s^3 = (d + s)(d^2 - ds + s^2) $$ -
State the final factorization
The completely factored form of the expression is:
$$ d^3 + s^3 = (d + s)(d^2 - ds + s^2) $$
The completely factored form of ( d^3 + s^3 ) is:
$$ (d + s)(d^2 - ds + s^2) $$
More Information
This expression represents the sum of two cubes. The factoring process helps in simplifying polynomial expressions, which is useful in algebra for solving equations and graphing.
Tips
- Forgetting the signs: When using the sum of cubes formula, remember that it specifically has a negative term ( -ab ) in the second factor.
- Not fully factoring: Ensure that you do not stop at the first factorization step; it must be expressed completely.
AI-generated content may contain errors. Please verify critical information