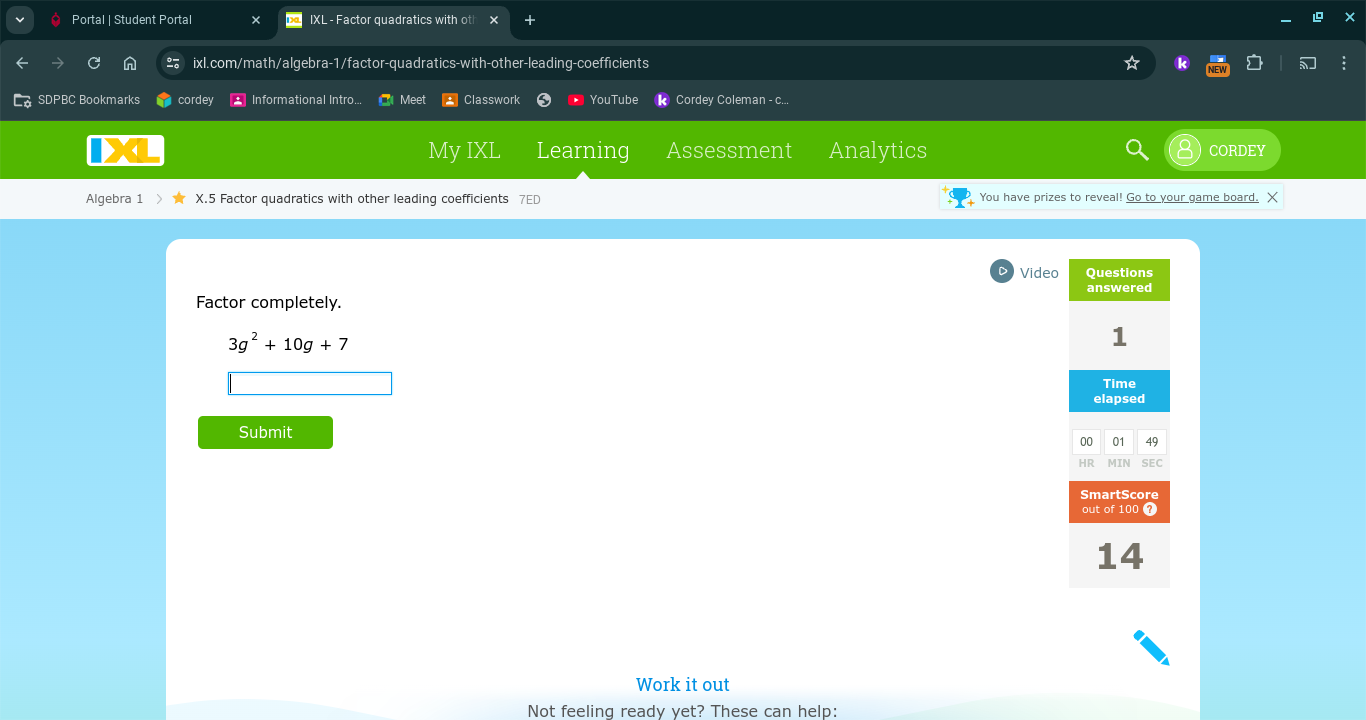
Factor completely: 3g² + 10g + 7.

Steps to Solve

1. Identify coefficients

In the quadratic expression $3g^2 + 10g + 7$, identify the coefficients:

• $a = 3$ (coefficient of $g^2$)
• $b = 10$ (coefficient of $g$)
• $c = 7$ (constant term)

2. Multiply ( a ) and ( c )

Multiply the coefficients $a$ and $c$ to find the product:

$$ ac = 3 \cdot 7 = 21 $$

3. Find factors of ( ac )

Look for two numbers that multiply to $21$ (the product we found) and add to $10$ (the coefficient ( b )). The numbers are $3$ and $7$ since:

$$ 3 \cdot 7 = 21 \quad \text{and} \quad 3 + 7 = 10 $$

4. Rewrite the middle term

Rewrite the expression using the numbers found to replace the middle term ( 10g ):

$$ 3g^2 + 3g + 7g + 7 $$

5. Factor by grouping

Group the first two terms and the last two terms:

$$ (3g^2 + 3g) + (7g + 7) $$

Now, factor each group:

$$ 3g(g + 1) + 7(g + 1) $$

6. Factor out the common binomial factor

Now we can factor out the common factor ((g + 1)):

$$ (3g + 7)(g + 1) $$