Factor a^3 + v^3 completely.
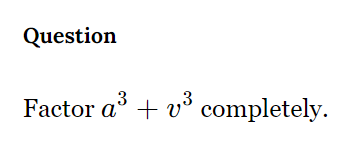
Understand the Problem
The question is asking to factor the expression a^3 + v^3 completely. This involves applying the algebraic identity for the sum of cubes.
Answer
The complete factorization of \( a^3 + v^3 \) is $$(a + v)(a^2 - av + v^2)$$.
Answer for screen readers
The complete factorization of ( a^3 + v^3 ) is $$(a + v)(a^2 - av + v^2)$$.
Steps to Solve
- Identify the Sum of Cubes Formula
The formula for factoring the sum of cubes is given by: $$ x^3 + y^3 = (x + y)(x^2 - xy + y^2) $$
In this case, we set ( x = a ) and ( y = v ).
- Apply the Formula to the Expression
Now substitute ( a ) and ( v ) into the formula: $$ a^3 + v^3 = (a + v)(a^2 - av + v^2) $$
- Write the Completely Factored Form
Thus, the complete factorization of ( a^3 + v^3 ) is: $$ a^3 + v^3 = (a + v)(a^2 - av + v^2) $$
The complete factorization of ( a^3 + v^3 ) is $$(a + v)(a^2 - av + v^2)$$.
More Information
The sum of cubes factorization is an important algebraic identity that helps simplify polynomial expressions. It can be utilized in various algebraic contexts, such as solving equations or performing polynomial long division.
Tips
- Forgetting the signs: When using the sum of cubes formula, ensure that the signs in the second factor are correct.
- Not recognizing it as a sum of cubes: Always check if the expression can be categorized as a sum of cubes before attempting to factor.
AI-generated content may contain errors. Please verify critical information