Exprimer le plus simple possible: 1. $\vec{AC} - \vec{BC}$ 2. $\vec{AD} - \vec{FD} + \vec{ED} - \vec{AF} + \vec{BE} + \vec{AB}$ 3. $\vec{FE} - \vec{GE} - \vec{GF} + \vec{GH} + \vec... Exprimer le plus simple possible: 1. $\vec{AC} - \vec{BC}$ 2. $\vec{AD} - \vec{FD} + \vec{ED} - \vec{AF} + \vec{BE} + \vec{AB}$ 3. $\vec{FE} - \vec{GE} - \vec{GF} + \vec{GH} + \vec{GF}$ 4. $\vec{AB} - \vec{BD} + \vec{CA} - \vec{CB}$ 5. $3 \times (\vec{AB} - 2\vec{DA}) - 2 \times (\vec{AB} - 3\vec{DA})$ Démontrer les égalités suivantes en utilisant la relation de Chasles: 1. $\vec{AC} + \vec{BD} = \vec{AD} + \vec{BC}$ 2. $\vec{BE} + \vec{CB} - \vec{DE} = \vec{CD}$
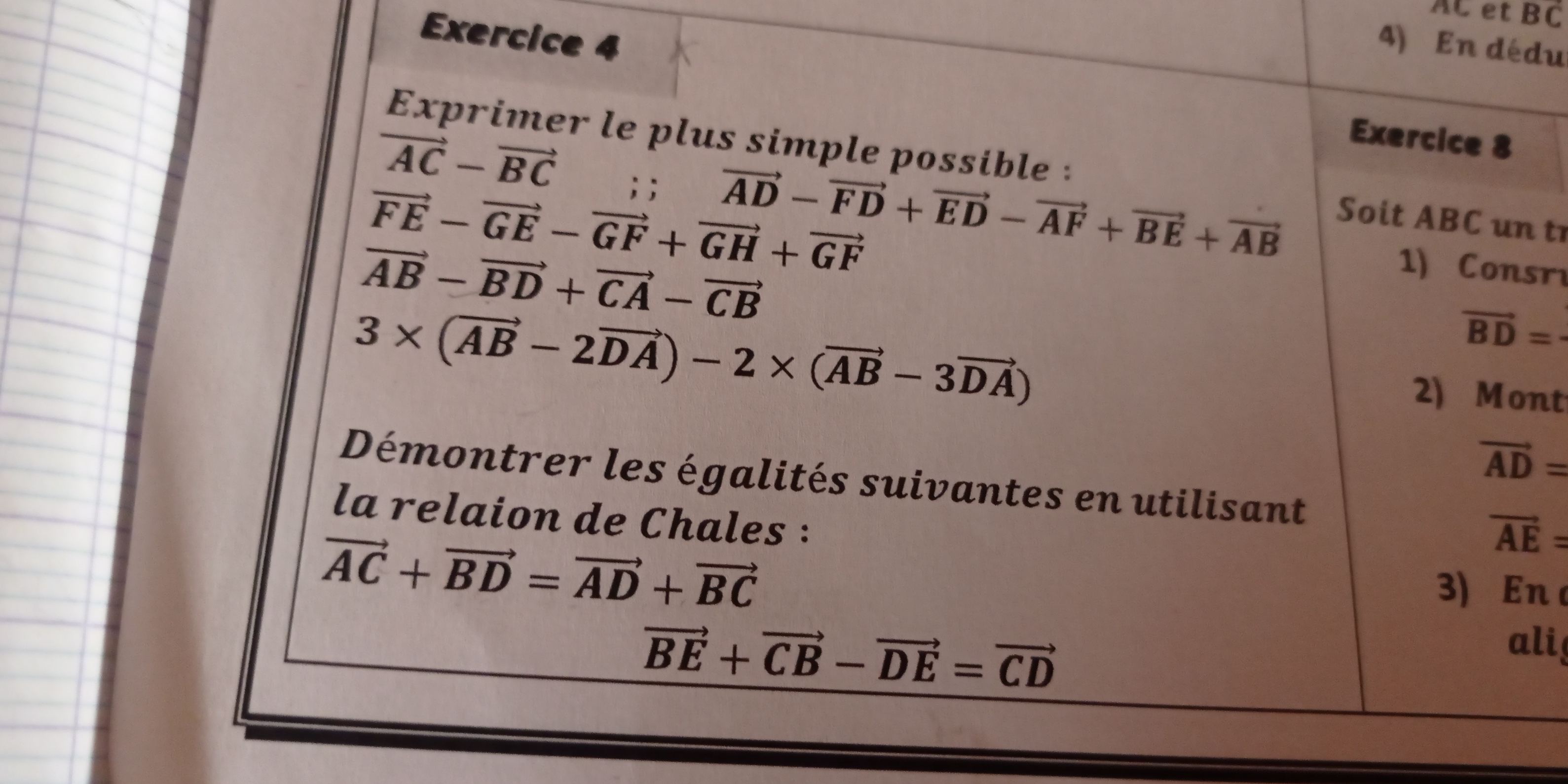
Understand the Problem
Il s'agit d'un exercice de géométrie vectorielle. La question demande d'exprimer les expressions vectorielles données de la manière la plus simple possible et de démontrer des égalités vectorielles en utilisant la relation de Chasles.
Answer
$\vec{AC} - \vec{BC} = \vec{AB}$ $\vec{AD} - \vec{FD} + \vec{ED} - \vec{AF} + \vec{BE} + \vec{AB} = \vec{AD}$ $\vec{FE} - \vec{GE} - \vec{GF} + \vec{GH} + \vec{GF} = \vec{FH}$ $\vec{AB} - \vec{BD} + \vec{CA} - \vec{CB} = \vec{DB}$ $3 \times (\vec{AB} - 2\vec{DA}) - 2 \times (\vec{AB} - 3\vec{DA}) = \vec{AB}$ $\vec{AC} + \vec{BD} = \vec{AD} + \vec{BC}$ $\vec{BE} + \vec{CB} - \vec{DE} = \vec{CD}$
Answer for screen readers
$\vec{AC} - \vec{BC} = \vec{AB}$ $\vec{AD} - \vec{FD} + \vec{ED} - \vec{AF} + \vec{BE} + \vec{AB} = \vec{AD}$ $\vec{FE} - \vec{GE} - \vec{GF} + \vec{GH} + \vec{GF} = \vec{FH}$ $\vec{AB} - \vec{BD} + \vec{CA} - \vec{CB} = \vec{DB}$ $3 \times (\vec{AB} - 2\vec{DA}) - 2 \times (\vec{AB} - 3\vec{DA}) = \vec{AB}$ $\vec{AC} + \vec{BD} = \vec{AD} + \vec{BC}$ $\vec{BE} + \vec{CB} - \vec{DE} = \vec{CD}$
Steps to Solve
-
Simplifier $\vec{AC} - \vec{BC}$ On peut réécrire l'expression comme $\vec{AC} + \vec{CB}$, car $-\vec{BC}=\vec{CB}$. Ensuite, par la relation de Chasles, $\vec{AC} + \vec{CB} = \vec{AB}$.
-
Simplifier $\vec{AD} - \vec{FD} + \vec{ED} - \vec{AF} + \vec{BE} + \vec{AB}$ On peut réécrire l'expression comme $\vec{AD} + \vec{DF} + \vec{ED} + \vec{FA} + \vec{BE} + \vec{AB}$. En regroupant, on a $\vec{AD} + \vec{DF} + \vec{FA} + \vec{AB} + \vec{BE} + \vec{ED}$. En utilisant la relation de Chasles: $\vec{AD} + \vec{DF} = \vec{AF}$, donc $\vec{AF} + \vec{FA} = \vec{AA} = \vec{0}$. Puis, $\vec{AB} + \vec{BE} = \vec{AE}$, donc $\vec{AE} + \vec{ED} = \vec{AD}$. Finalement, la somme est $\vec{0} + \vec{AD} = \vec{AD}$.
-
Simplifier $\vec{FE} - \vec{GE} - \vec{GF} + \vec{GH} + \vec{GF}$ On peut réécrire l'expression comme $\vec{FE} + \vec{EG} + \vec{FG} + \vec{GH} + \vec{GF}$. En regroupant, on a $\vec{FE} + \vec{EG} + \vec{FG} + \vec{GF} + \vec{GH}$. Puis, $\vec{FG} + \vec{GF} = \vec{FF} = \vec{0}$. Ensuite, $\vec{FE} + \vec{EG} = \vec{FG}$, donc $\vec{FG} + \vec{0} + \vec{GH} = \vec{FG} + \vec{GH} = \vec{FH}$.
-
Simplifier $\vec{AB} - \vec{BD} + \vec{CA} - \vec{CB}$ On peut réécrire l'expression comme $\vec{AB} + \vec{DB} + \vec{CA} + \vec{BC}$. En regroupant, on a $\vec{AB} + \vec{BC} + \vec{CA} + \vec{DB}$. Puis, $\vec{AB} + \vec{BC} = \vec{AC}$, donc $\vec{AC} + \vec{CA} = \vec{AA} = \vec{0}$. Finalement, la somme est $\vec{0} + \vec{DB} = \vec{DB}$.
-
Simplifier $3 \times (\vec{AB} - 2\vec{DA}) - 2 \times (\vec{AB} - 3\vec{DA})$ Développons l'expression: $3\vec{AB} - 6\vec{DA} - 2\vec{AB} + 6\vec{DA}$. On regroupe les termes semblables : $(3\vec{AB} - 2\vec{AB}) + (-6\vec{DA} + 6\vec{DA}) = \vec{AB} + \vec{0} = \vec{AB}$.
-
Démontrer $\vec{AC} + \vec{BD} = \vec{AD} + \vec{BC}$ On peut réécrire $\vec{AC}$ comme $\vec{AD} + \vec{DC}$ et $\vec{BD}$ comme $\vec{BC} + \vec{CD}$. Donc, $\vec{AC} + \vec{BD} = \vec{AD} + \vec{DC} + \vec{BC} + \vec{CD} = \vec{AD} + \vec{BC} + \vec{DC} + \vec{CD} = \vec{AD} + \vec{BC} + \vec{0} = \vec{AD} + \vec{BC}$.
-
Démontrer $\vec{BE} + \vec{CB} - \vec{DE} = \vec{CD}$ On peut réécrire $-\vec{DE}$ comme $\vec{ED}$. Donc, $\vec{BE} + \vec{CB} + \vec{ED} = \vec{BE} + \vec{ED} + \vec{CB}$. Puis, $\vec{BE} + \vec{ED} = \vec{BD}$, donc $\vec{BD} + \vec{CB} = \vec{CB} + \vec{BD}$. Maintenant, on peut réécrire $\vec{BD}$ comme $\vec{CD} + \vec{BC}$. Donc, $\vec{CB} + \vec{CD} + \vec{BC} = \vec{CD} + \vec{CB} + \vec{BC} = \vec{CD} + \vec{0} = \vec{CD}$.
$\vec{AC} - \vec{BC} = \vec{AB}$ $\vec{AD} - \vec{FD} + \vec{ED} - \vec{AF} + \vec{BE} + \vec{AB} = \vec{AD}$ $\vec{FE} - \vec{GE} - \vec{GF} + \vec{GH} + \vec{GF} = \vec{FH}$ $\vec{AB} - \vec{BD} + \vec{CA} - \vec{CB} = \vec{DB}$ $3 \times (\vec{AB} - 2\vec{DA}) - 2 \times (\vec{AB} - 3\vec{DA}) = \vec{AB}$ $\vec{AC} + \vec{BD} = \vec{AD} + \vec{BC}$ $\vec{BE} + \vec{CB} - \vec{DE} = \vec{CD}$
More Information
La relation de Chasles est un outil fondamental en géométrie vectorielle. Elle permet de simplifier et de manipuler des expressions vectorielles en décomposant les vecteurs en sommes de vecteurs intermédiaires.
Tips
- Oublier de changer le signe lorsqu'on inverse un vecteur, par exemple, $-\vec{BC} = \vec{CB}$.
- Ne pas appliquer correctement la relation de Chasles.
- Faire des erreurs de calcul lors de la simplification des expressions algébriques vectorielles.
AI-generated content may contain errors. Please verify critical information