Express $2^{122} \times 5^{120}$ in standard form.
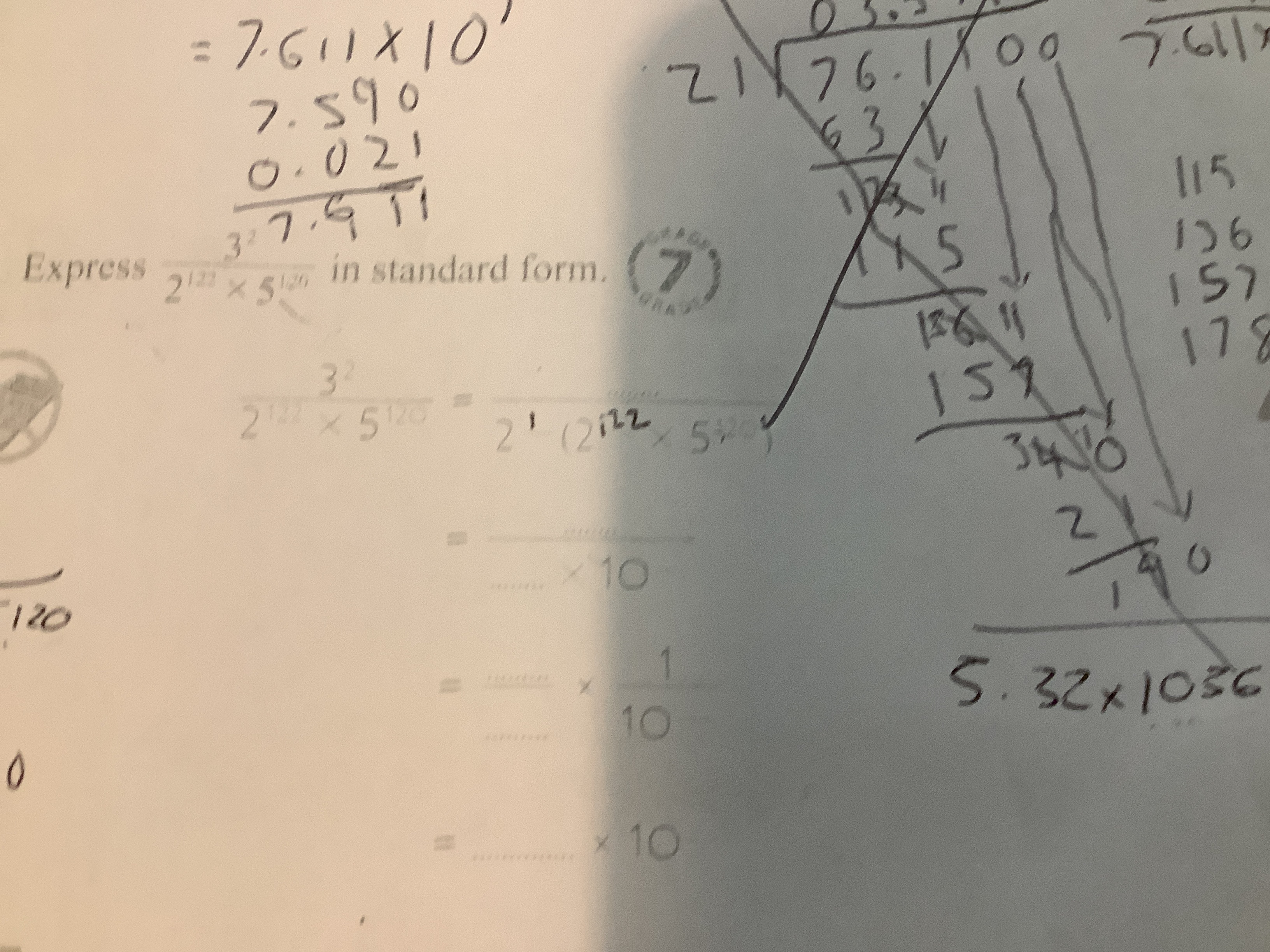
Understand the Problem
The question asks to express the number $2^{122} \times 5^{120}$ in standard form. This requires applying the properties of exponents and standard notation techniques.
Answer
$4 \times 10^{120}$
Answer for screen readers
$4 \times 10^{120}$
Steps to Solve
- Rewrite the expression
We start by rewriting the given expression $2^{122} \times 5^{120}$.
- Separate the terms with same exponent
Use the properties of exponents to combine terms: $2^{122} \times 5^{120} = 2^2 \times 2^{120} \times 5^{120}$
- Combine similar exponents
Now, combine $2^{120}$ and $5^{120}$ to get $(2 \times 5)^{120}$: $2^{122} \times 5^{120} = 2^2 \times (2 \times 5)^{120} = 4 \times (10)^{120}$
- Express in standard form
The number $4 \times 10^{120}$ is already in standard form, which is $a \times 10^n$ where $1 \le a < 10$ and $n$ is an integer. In this case, $a = 4$ and $n = 120$. Therefore, the standard form is just $4 \times 10^{120}$.
$4 \times 10^{120}$
More Information
Standard form, also known as scientific notation, is a way of writing down very large or very small numbers easily. It is written as $a \times 10^n$, where $1 \le |a| < 10$ and $n$ is an integer.
Tips
A common mistake would be incorrectly applying the exponent rules or not recognizing when the number is already in standard form. For instance, one might try to further manipulate $4 \times 10^{120}$ unnecessarily.
AI-generated content may contain errors. Please verify critical information