Expand the expression to a polynomial in standard form: (3x + 2)(3x² - 3x - 7)
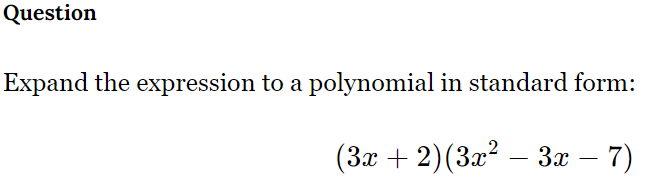
Understand the Problem
The question is asking to expand the expression (3x + 2)(3x² - 3x - 7) into a polynomial and write it in standard form.
Answer
The expanded form is \( 9x^3 - 3x^2 - 27x - 14 \).
Answer for screen readers
The expanded expression in standard form is ( 9x^3 - 3x^2 - 27x - 14 ).
Steps to Solve
- Distributing the first term of the first binomial
Start by distributing the first term ( 3x ) from the first binomial ( (3x + 2) ) to each term in the second binomial ( (3x^2 - 3x - 7) ).
[ 3x \cdot 3x^2 = 9x^3 ] [ 3x \cdot (-3x) = -9x^2 ] [ 3x \cdot (-7) = -21x ]
- Distributing the second term of the first binomial
Now distribute the second term ( 2 ) from the first binomial ( (3x + 2) ) to each term in the second binomial ( (3x^2 - 3x - 7) ).
[ 2 \cdot 3x^2 = 6x^2 ] [ 2 \cdot (-3x) = -6x ] [ 2 \cdot (-7) = -14 ]
- Combining like terms
Add all the terms from steps 1 and 2 together and combine like terms.
[ 9x^3 + (-9x^2 + 6x^2) + (-21x - 6x) - 14 ]
This simplifies to:
[ 9x^3 - 3x^2 - 27x - 14 ]
- Writing in standard form
Ensure the polynomial is written in standard form, which arranges terms by descending powers of ( x ).
The standard form is:
[ 9x^3 - 3x^2 - 27x - 14 ]
The expanded expression in standard form is ( 9x^3 - 3x^2 - 27x - 14 ).
More Information
The process of expanding a binomial expression involves distributing each term of one binomial across all terms of the other binomial. This technique ensures that each term is accounted for in the final polynomial.
Tips
- Neglecting to distribute all terms correctly.
- Forgetting to combine like terms properly.
- Writing terms in a non-standard order (not arranging by decreasing powers of ( x )).
AI-generated content may contain errors. Please verify critical information