Expand the expression: (4 - b)(5b^2 + 5b - 4)
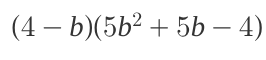
Understand the Problem
The question requires expanding the expression (4 - b)(5b^2 + 5b - 4). This involves multiplying each term in the first parentheses by each term in the second parentheses, and then simplifying by combining like terms.
Answer
$-5b^3 + 15b^2 + 24b - 16$
Answer for screen readers
$-5b^3 + 15b^2 + 24b - 16$
Steps to Solve
-
Distribute 4 Multiply 4 by each term in the second parenthesis: $4 * (5b^2 + 5b - 4) = 20b^2 + 20b - 16$
-
Distribute -b Multiply -b by each term in the second parenthesis: $-b * (5b^2 + 5b - 4) = -5b^3 - 5b^2 + 4b$
-
Combine the results Add the results from step 1 and step 2: $(20b^2 + 20b - 16) + (-5b^3 - 5b^2 + 4b) = -5b^3 + (20b^2 - 5b^2) + (20b + 4b) - 16$
-
Simplify Combine like terms: $-5b^3 + 15b^2 + 24b - 16$
$-5b^3 + 15b^2 + 24b - 16$
More Information
The expanded form of the given expression is a cubic polynomial.
Tips
A common mistake is not paying attention to the signs when distributing. Also, errors can occur when combining like terms, particularly if the terms are not written in a clear order.
AI-generated content may contain errors. Please verify critical information