Expand: (t-2)(t+5)

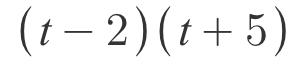
Understand the Problem

The question requires to expand the product of two binomials. This involves multiplying each term of the first binomial by each term of the second binomial and then simplifying the resulting expression.

Answer

$t^2 + 3t - 10$

Steps to Solve

Expand the product using the distributive property (FOIL method)

Multiply each term in the first binomial $(t-2)$ by each term in the second binomial $(t+5)$.

$(t-2)(t+5) = t(t+5) - 2(t+5)$

Distribute $t$ and $-2$

$t(t+5) = t^2 + 5t$ $-2(t+5) = -2t - 10$

So, the expression becomes: $t^2 + 5t - 2t - 10$

Combine like terms

Combine the $5t$ and $-2t$ terms:

$5t - 2t = 3t$

The expression simplifies to: $t^2 + 3t - 10$

$t^2 + 3t - 10$

More Information

The expanded form of $(t-2)(t+5)$ is $t^2 + 3t - 10$. This is a quadratic expression.

Tips

A common mistake is to forget to multiply each term in the first binomial by each term in the second binomial during the expansion process. For example, some might forget to multiply $-2$ by $5$, resulting in an incorrect answer.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!