Expand (3r - 2)^2
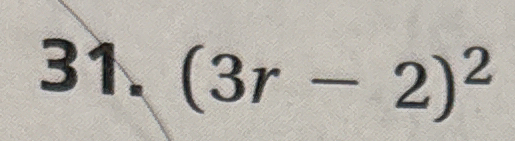
Understand the Problem
The question requires us to expand the binomial expression (3r - 2)^2. We will use the formula (a - b)^2 = a^2 - 2ab + b^2 to achieve this.
Answer
$9r^2 - 12r + 4$
Answer for screen readers
$9r^2 - 12r + 4$
Steps to Solve
- Identify a and b
In the expression $(3r - 2)^2$, we can identify $a = 3r$ and $b = 2$.
- Apply the formula $(a - b)^2 = a^2 - 2ab + b^2$
Substitute $a = 3r$ and $b = 2$ into the formula: $$ (3r - 2)^2 = (3r)^2 - 2(3r)(2) + (2)^2 $$
- Simplify each term
Square the first term: $(3r)^2 = 9r^2$. Multiply the terms in the middle: $2(3r)(2) = 12r$. Square the last term: $(2)^2 = 4$.
- Combine the simplified terms
Substitute the simplified terms back into the expression: $$ (3r - 2)^2 = 9r^2 - 12r + 4 $$
$9r^2 - 12r + 4$
More Information
The binomial expansion of $(3r - 2)^2$ results in a quadratic expression.
Tips
A common mistake is forgetting to multiply the middle term by 2, or incorrectly squaring the terms. Ensure each term is properly squared and multiplied. For example, students may forget to square the 3 in $(3r)^2$, yielding an incorrect $3r^2$ instead of $9r^2$. Also, watch the signs.
AI-generated content may contain errors. Please verify critical information