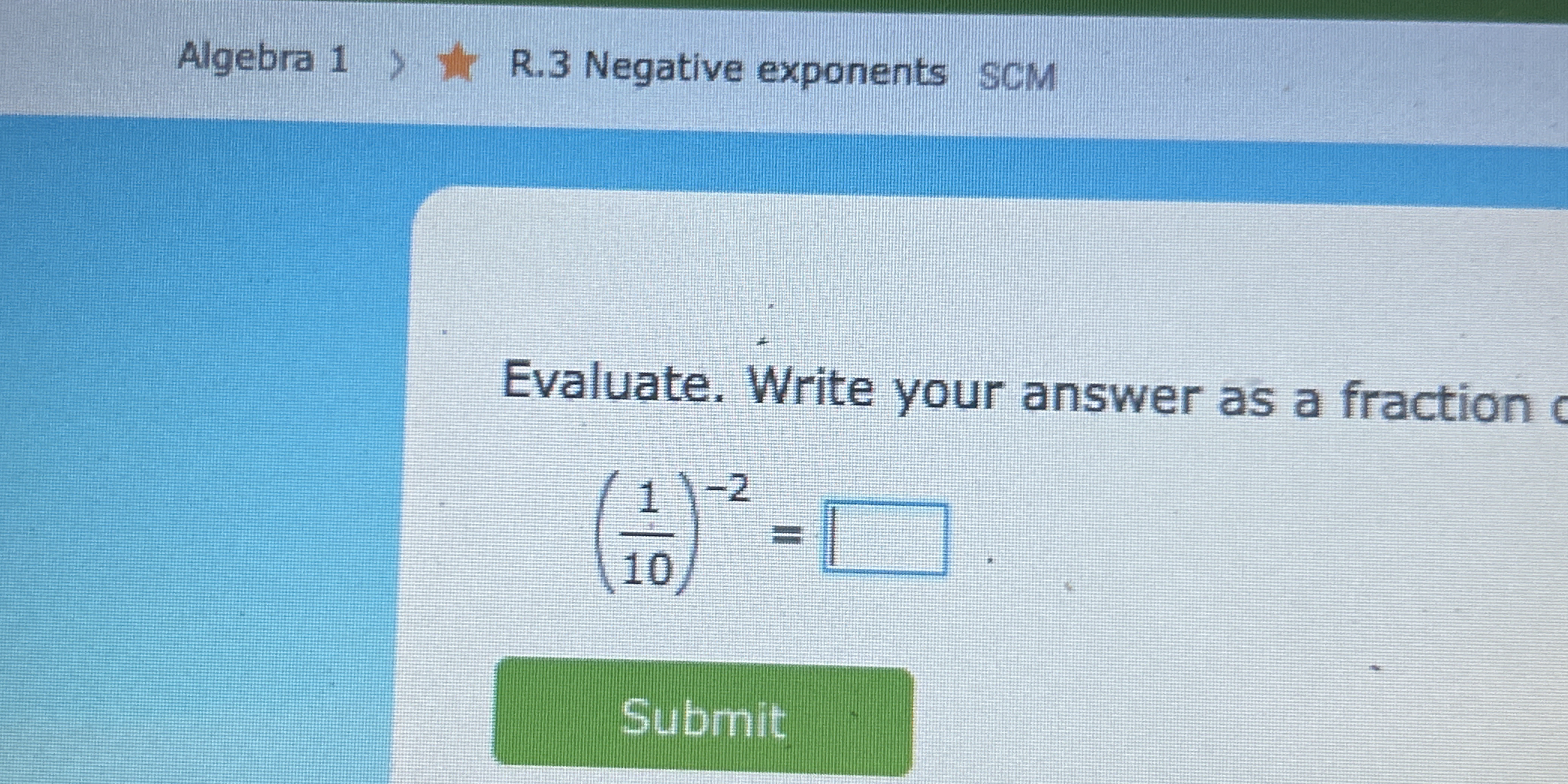
Evaluate. Write your answer as a fraction of (1/10)^-2 =
Understand the Problem
The question is asking to evaluate the expression \((\frac{1}{10})^{-2} \) and provide the answer as a fraction.
Answer
The answer is \( \frac{100}{1} \).
Answer for screen readers
The evaluated expression is ( \frac{100}{1} ).
Steps to Solve
- Understanding Negative Exponents
Recall that a negative exponent means to take the reciprocal of the base and change the exponent to positive. In this case, we apply it to the expression ( \left(\frac{1}{10}\right)^{-2} ).
- Taking the Reciprocal
Taking the reciprocal of ( \frac{1}{10} ) gives you ( 10 ). So we rewrite the expression as:
$$ \left(\frac{1}{10}\right)^{-2} = 10^{2} $$
- Calculating ( 10^{2} )
Now, calculate ( 10^{2} ):
$$ 10^{2} = 10 \times 10 = 100 $$
- Expressing as a Fraction
Since the question requires the answer as a fraction, we can express ( 100 ) as:
$$ \frac{100}{1} $$
The evaluated expression is ( \frac{100}{1} ).
More Information
The expression ( \left(\frac{1}{10}\right)^{-2} ) demonstrates how negative exponents work, transforming a fraction into a whole number by taking the reciprocal and squaring it.
Tips
- Ignoring the Reciprocal: A common mistake is to forget to take the reciprocal when dealing with negative exponents.
- Miscalculating Powers: Be mindful when squaring numbers; ensure that you multiply correctly.
AI-generated content may contain errors. Please verify critical information