Evaluate the limits of r(x) as x approaches specific values.
Understand the Problem
The question involves limits of a function r(x) as x approaches values, asking for evaluations at specific points. It seems to present a comparison of limits from both the left and right towards a specific value.
Answer
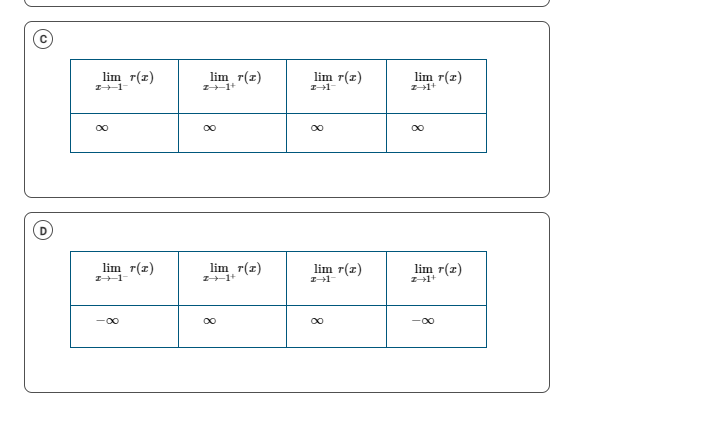
The limits are \( \lim_{x \to -1^-} r(x) = \infty \), \( \lim_{x \to -1^+} r(x) = \infty \), and \( \lim_{x \to -1} r(x) = \infty \).
Answer for screen readers
The values for the limits are:
- ( \lim_{x \to -1^-} r(x) = \infty )
- ( \lim_{x \to -1^+} r(x) = \infty )
- ( \lim_{x \to -1} r(x) = \infty )
Steps to Solve
-
Understanding One-Sided Limits
To evaluate the limits as ( x ) approaches ( -1 ) from the left and right, we need to analyze ( r(x) ) for values just left of ( -1 ) (denoted as ( r(-1^-) )) and just right of ( -1 ) (denoted as ( r(-1^+) )).
-
Evaluate ( \lim_{x \to -1^-} r(x) )
This limit checks the behavior of ( r(x) ) as ( x ) approaches ( -1 ) from the left side. If we observe ( r(x) ) approaching ( \infty ) from this direction, we record ( \lim_{x \to -1^-} r(x) = \infty ).
-
Evaluate ( \lim_{x \to -1^+} r(x) )
Similarly, check ( r(x) ) by approaching ( -1 ) from the right. If this limit also approaches ( \infty ), we write ( \lim_{x \to -1^+} r(x) = \infty ).
-
Consider the Two-Sided Limit
For the two-sided limit ( \lim_{x \to -1} r(x) ) to exist, both the left-hand limit and right-hand limit must equal each other. Since both are ( \infty ), we conclude ( \lim_{x \to -1} r(x) = \infty ).
-
Evaluate Remaining Limits as ( x ) approaches Values
Repeat the process for other values, if necessary (for example, checking limits as ( x ) approaches other values near ( -1 ) or ( \infty ) or ( -\infty )).
The values for the limits are:
- ( \lim_{x \to -1^-} r(x) = \infty )
- ( \lim_{x \to -1^+} r(x) = \infty )
- ( \lim_{x \to -1} r(x) = \infty )
More Information
In calculus, the behavior of functions near certain points, especially at points of discontinuity or infinity, is critical for understanding overall function behavior. One-sided limits help delineate how the function approaches a value from different directions.
Tips
- Ignoring one-sided limits: It's essential to evaluate both the left-hand and right-hand limits separately.
- Assuming the two-sided limit exists: Ensure both one-sided limits are equal before concluding the two-sided limit.
AI-generated content may contain errors. Please verify critical information