Evaluate the integral of (x² + 4x³ + 2) / (6x) dx
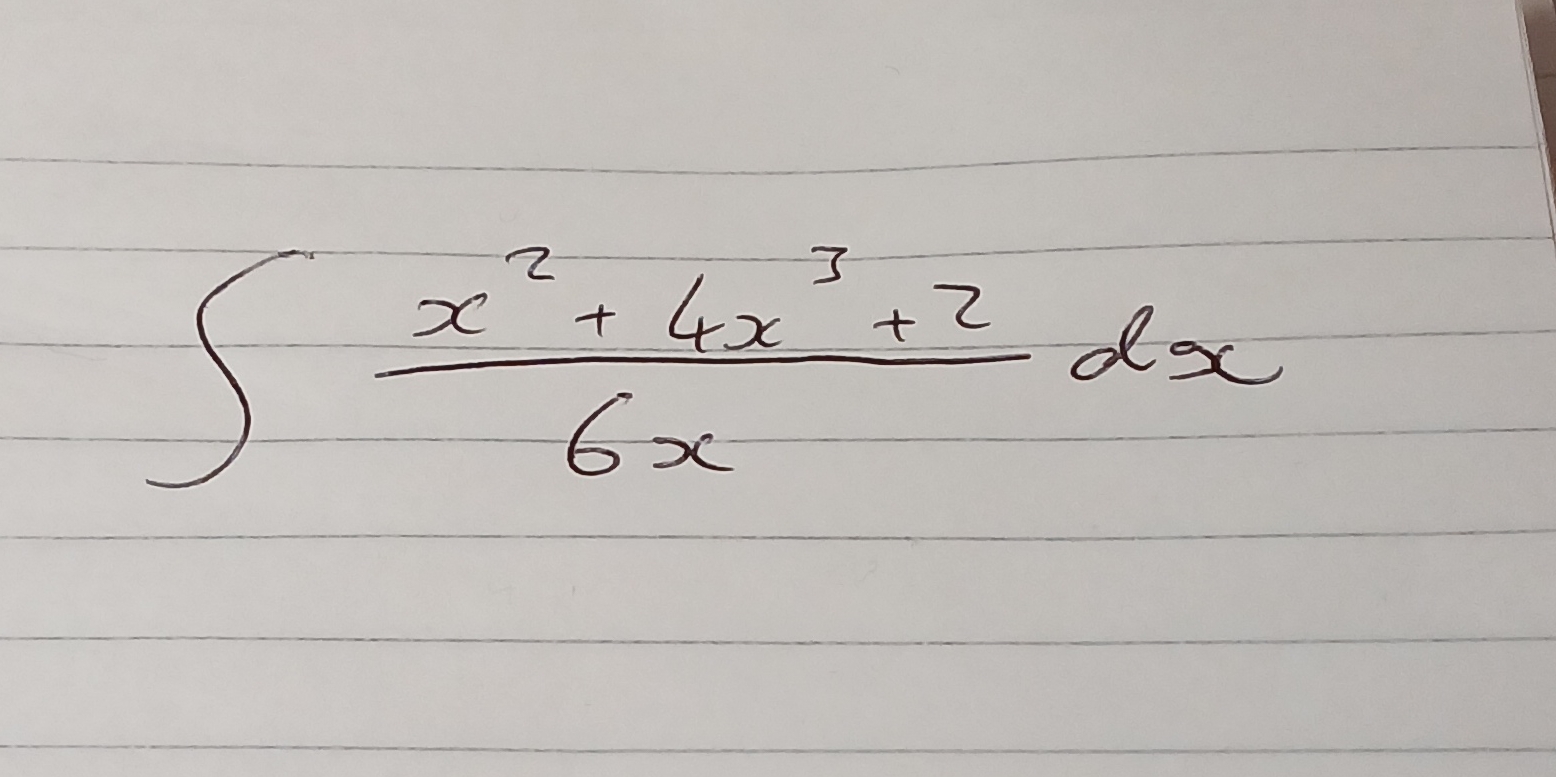
Understand the Problem
The question is asking to evaluate the integral of the expression (x² + 4x³ + 2) / (6x) with respect to x. This involves integrating a rational function, which requires simplification and applying integration rules.
Answer
$$ \frac{x^2}{12} + \frac{2x^3}{9} + \frac{1}{3} \ln|x| + C $$
Answer for screen readers
$$ \int \frac{x^2 + 4x^3 + 2}{6x} , dx = \frac{x^2}{12} + \frac{2x^3}{9} + \frac{1}{3} \ln|x| + C $$
Steps to Solve
- Simplify the integral expression
Start by simplifying the fraction inside the integral: $$ \frac{x^2 + 4x^3 + 2}{6x} = \frac{x^2}{6x} + \frac{4x^3}{6x} + \frac{2}{6x} $$ This simplifies to: $$ \frac{x}{6} + \frac{2}{3}x^2 + \frac{1}{3x} $$
- Rewrite the integral
Now we rewrite the integral using the simplified expression: $$ \int \left( \frac{x}{6} + \frac{2}{3}x^2 + \frac{1}{3x} \right) dx $$
- Integrate each term separately
Integrate each term individually:
-
For $\frac{x}{6}$: $$ \int \frac{x}{6} , dx = \frac{1}{6} \cdot \frac{x^2}{2} = \frac{x^2}{12} $$
-
For $\frac{2}{3}x^2$: $$ \int \frac{2}{3}x^2 , dx = \frac{2}{3} \cdot \frac{x^3}{3} = \frac{2x^3}{9} $$
-
For $\frac{1}{3x}$: $$ \int \frac{1}{3x} , dx = \frac{1}{3} \ln|x| $$
- Combine the results
Adding all the parts together gives us: $$ \int \left( \frac{x}{6} + \frac{2}{3} x^2 + \frac{1}{3x} \right) dx = \frac{x^2}{12} + \frac{2x^3}{9} + \frac{1}{3}\ln|x| + C $$
Where (C) is the constant of integration.
$$ \int \frac{x^2 + 4x^3 + 2}{6x} , dx = \frac{x^2}{12} + \frac{2x^3}{9} + \frac{1}{3} \ln|x| + C $$
More Information
This integral showcases the technique of breaking down rational functions into simpler components that can be integrated independently. It combines polynomial and logarithmic integration, which are essential techniques in calculus.
Tips
- Not simplifying the rational expression before integrating, which can lead to unnecessary complexity.
- Forgetting to include the constant of integration after finding the indefinite integral.
